题目内容
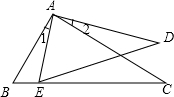如图∠1=∠2，∠C=∠D，求证：AB•AD=AC•AE．考点：相似三角形的判定与性质
专题：证明题
分析：由条件证明△ABC∽△AED，再利用相似三角形的性质可得出结论．
解答：证明：∵∠1=∠2，
∴∠1+∠EAC=∠2+∠EAC，
即∠BAC=∠EAD，且∠C=∠D，
∴△ABC∽△AED，
∴
=
，
∴AB•AD=AC•AE．
∴∠1+∠EAC=∠2+∠EAC，
即∠BAC=∠EAD，且∠C=∠D，
∴△ABC∽△AED，
∴
| AB |
| AE |
| AC |
| AD |
∴AB•AD=AC•AE．
点评：本题主要考查相似三角形的判定和性质，掌握相似三角形的判定方法是解题的关键，化线段的积为比例证三角形相似是解决这类问题的常用方法．
练习册系列答案
相关题目
设a、b是任意两个实数，且a＜b．我们规定：满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间，表示为[a，b]．对于一个函数，如果它的自变量x与函数值y满足：当a≤x≤b时，有a≤y≤b，我们就称此函数是闭区间[a，b]上的“闭函数”．若二次函数y=
x2-2x是区间[m，n]上的“闭函数”，则实数m、n值分别为（ ）
| 1 |
| 2 |
A、m=1-
| ||||
B、m=-1，n=2或m=1-
| ||||
| C、m=-2，n=6 | ||||
D、m=-2，n=6或m=1-
|
如图，在Rt△ABC中，∠C=90°，BC=5，若以点C为圆心，CB长为半径的圆恰好经过AB的中点D，则AB的长等于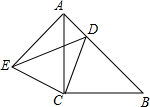
如图，△ACB和△ECD都是等腰直角三形，且∠ACB=∠ECD=90°，求证：
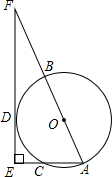如图，AB是⊙O的直径，AC为弦，D是