题目内容
 如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:
如图,⊙C经过原点且与两坐标轴分别交于点A和点B,点A的坐标为(0,2),D为⊙C在第一象限内的一点且∠ODB=60°,解答下列各题:(1)求圆的半径;
(2)求圆心C的坐标.
考点:圆周角定理,坐标与图形性质,解直角三角形
专题:
分析:(1)连接AB,判断出∠OAB=60°,从而得到∠OBA=30°,根据AB=2OA=4,可求出⊙C的半径r=2.
(2)在Rt△OAB中,由勾股定理得到OB的长,再根据垂径定理求出OE、OF的长,从而得到C点坐标.
(2)在Rt△OAB中,由勾股定理得到OB的长,再根据垂径定理求出OE、OF的长,从而得到C点坐标.
解答:
 解(1)连接AB,
解(1)连接AB,
∵∠ODB=∠OAB,∠ODB=60°,
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,∠OBA=30°,
∴AB=2OA=4,
∴⊙C的半径r=2.
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,
∴OB=2
,
过C点作CE⊥OA于E,CF⊥OB于F,由垂径定理得:OE=AE=1,OF=BF=
,
∴CE=
,CF=1,
∴C的坐标为(
,1).
 解(1)连接AB,
解(1)连接AB,∵∠ODB=∠OAB,∠ODB=60°,
∴∠OAB=60°,
∵∠AOB是直角,
∴AB是⊙C的直径,∠OBA=30°,
∴AB=2OA=4,
∴⊙C的半径r=2.
(2)在Rt△OAB中,由勾股定理得:OB2+OA2=AB2,
∴OB=2
| 3 |
过C点作CE⊥OA于E,CF⊥OB于F,由垂径定理得:OE=AE=1,OF=BF=
| 3 |
∴CE=
| 3 |
∴C的坐标为(
| 3 |
点评:本题考查了圆周角定理、坐标与图形的性质,在圆中找到各定理的适用条件是解题的关键.

练习册系列答案
相关题目
如图1,圆的周长为4个单位.在该圆的4等分点处分别标上字母m、n、p、q.如图2,先将圆周上表示p的点与数轴原点重合,然后将该圆沿着数轴的负方向滚动,则数轴上表示-2013的点与圆周上重合的点对应的字母是( )


| A、m | B、n | C、p | D、q |
数轴上表示-1.5与
的两点之间,表示整数的点的个数是( )
| 9 |
| 2 |
| A、6 | B、5 | C、4 | D、3 |
两个多边形相似的条件是( )
| A、对应角相等 |
| B、对应边成比例 |
| C、对应角相等或对应边成比例 |
| D、对应角相等且对应边成比例 |
 如图,⊙O的直径CD垂直于弦EF,垂足为G,若∠EOD=40°,则∠CDF等于( )
如图,⊙O的直径CD垂直于弦EF,垂足为G,若∠EOD=40°,则∠CDF等于( )| A、80° | B、70° |
| C、40° | D、20° |
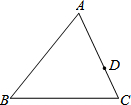 如图,在△ABC中,∠C>∠B,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为
如图,在△ABC中,∠C>∠B,AB=12,AC=9,D是AC上一点,AD=6,在AB上取一点E,使以A,D,E三点为顶点的三角形与△ABC相似,则AE的长为
 如图,四边形ABCD,∠ABC与∠DCE的平分线交于P.
如图,四边形ABCD,∠ABC与∠DCE的平分线交于P.