题目内容
6．若a=2+$\sqrt{5}$，b=$\frac{1}{2-\sqrt{5}}$，那么a与b的关系是（ ）| A． | a＜b且互为相反数 | B． | a＞b且a与b互为相反数 | ||
| C． | a＞b | D． | a=b |
分析 根据平方差公式，可对b分母有理化，根据相反数的定义、有理数的大小比较，可得答案．
解答 解：b=$\frac{2+\sqrt{5}}{（2-\sqrt{5}）（2+\sqrt{5}）}$=-2-$\sqrt{5}$，
a+b=2+$\sqrt{5}$-2-$\sqrt{5}$=0，
a、b互为相反数，
2+$\sqrt{5}$＞0＞-2-$\sqrt{5}$，
即a＞0＞b．
故选：B．
点评 本题考查了分母有理化，利用分数的性质分子分母都乘以分母中这两个数的差得出平方差公式是解题关键．
练习册系列答案
相关题目
如图，已知AD∥BC，∠DBC与∠C互余，BD平分∠ABC，∠A=112°，
在△ABC中，∠A=90°，点D在AC上，BD平分∠ABC，AD=10cm，求点D到BC的距离是多少？
14．方程x2-3x=0的根是（ ）
| A． | x=3 | B． | x1=3，x2=-3 | C． | x1=$\sqrt{3}$，x2=-$\sqrt{3}$ | D． | x1=0，x2=3 |
如图，△ABC的∠B与∠C的外角平分线相交于D点，∠A=50°，则∠D=75°．
如图，四边形ABCD是菱形，BC=5cm，BD=6cm，DH⊥AB于点H，则DH=4.8cm．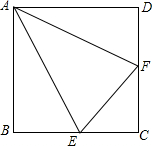
如图，在边长为2的正方形ABCD中，点E，F分别是BC，CD的中点，连接AE，AF，EF可得△AEF，求AE-EF的值．