如图.在平行四边形ABCD中.E.F分别为边AB.CD上的点.且DF=BE.连接DE.BF．求证:△ADE≌△CBF．题目和参考答案——青夏教育精英家教网—

题目内容

4．

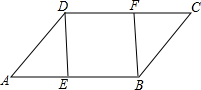如图，在平行四边形ABCD中，E、F分别为边AB、CD上的点，且DF=BE，连接DE、BF．求证：△ADE≌△CBF．

分析直接利用平行四边形的性质得出AB=DC，∠A=∠C，AD=BC，进而结合全等三角形的判定方法得出答案．

解答证明：∵四边形ABCD是平行四边形，
∴AB=DC，∠A=∠C，AD=BC，
∵DF=BE，
∴FC=AE，
在△ADE和△CBF中
$\left\{\begin{array}{l}{AD=BC}\\{∠A=∠C}\\{AE=FC}\end{array}\right.$，
∴△ADE≌△CBF（SAS）．

点评此题主要考查了平行四边形的性质以及全等三角形的判定，正确应用平行四边形的性质是解题关键．

练习册系列答案

相关题目

14．

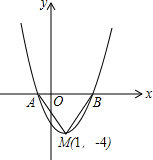如图是二次函数y=（x-1）²-4的图象，与x轴交于A，B两点．将二次函数的图象在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新的图象，请你结合这个新的图象回答：当直线y=x+b（b＜1）与此图象有两个公共点时，b的取值范围．

15．

点F为?ABCD中DC边上的点，连接AF并延长交BC的延长线于E点，并且交BD于G，求证：AG²=FG•EG．

12．

如图，抛物线y=x²+bx+c与x轴交A（-1、0）、B（3，0）两点，与y轴交于点C，顶点为D．
（1）求抛物线的解析式；
（2）抛物线上有一动点M，在抛物线的对称轴上是否存在一点N，使以A，B，M，N为顶点的四边形是平行四边形，若存在直接写出M点的坐标．

19．计算：16+（-25）+24-15．

9．

A、B、C、D四位同事去茶馆喝茶，现A已入坐，B、C、D三人将随机坐到其余三个位置上．若A希望与D相邻而坐，那么他实现愿望的概率为多少？（要求画树状图列出所有的可能情况）

16．计算：
（1）（$\sqrt{40}$-$\sqrt{\frac{2}{5}}$）×$\sqrt{10}$；
（2）（$\sqrt{24}$-$\sqrt{\frac{1}{6}}$）÷$\sqrt{3}$；
（3）$\frac{\sqrt{27}+\sqrt{12}}{\sqrt{3}}$-2；
（4）$\sqrt{8}$+4$\sqrt{\frac{1}{2}}$-$\sqrt{18}$．

13．根据下列条件，分别求出对应的二次函数的关系式．
（1）已知抛物线的顶点为（1，-3），且与y轴交于点（0，1）；
（2）已知抛物线与x轴交于点M（-3，0）、（5，0），且与y轴交于点（0，15）．

14．

如图，已知AB=AE，BC=ED，CF=FD，AC=AD．求证：∠BAF=∠EAF．

试题分类