题目内容
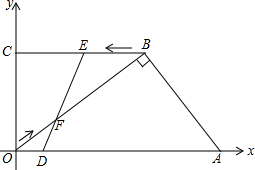 如图,在平面直角坐标系中,A(
如图,在平面直角坐标系中,A(| 25 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
(1)连接EF并延长交OA于点D,当E点运动到几秒时,四边形ABED是平行四边形?并求出此时平行四边形的面积.
(2)动点E、F是否会在某个反比例函数图象上?如果会,请求出这时动点E、F运动的时间t的值,并求出该反比例函数的表达式;如果不会,请说明理由.
考点:反比例函数综合题
专题:
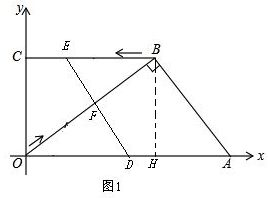
分析:(1)设E点运动到t秒时,四边形ABED是平行四边形,过点B作BH⊥OA于H,如图1,易证△OHB∽△OBA,从而可求出OH、BH的值,易证△BFE∽△OHB,根据相似三角形的性质可求出t的值,也就可求出平行四边形的面积;
(2)过点F作FG⊥OA于G,如图2,易证△OGF∽△OHB,根据相似三角形的性质可用t表示出点F的坐标,然后只需求出点E的坐标(用t表示),再运用待定系数法就可解决问题.
(2)过点F作FG⊥OA于G,如图2,易证△OGF∽△OHB,根据相似三角形的性质可用t表示出点F的坐标,然后只需求出点E的坐标(用t表示),再运用待定系数法就可解决问题.
解答:解:(1)设E点运动到t秒时,四边形ABED是平行四边形,过点B作BH⊥OA于H,如图1,
则有BE=
t,OF=
t,BF=10-
t,BE∥AD,DE∥AB,∠OHB=90°.
∵∠OBA=90°,
∴∠OHB=∠OBA.
又∵∠BOH=∠AOB,
∴△OHB∽△OBA,
∴
=
,
∴OB2=OH•OA.
∵A(
,0)即OA=
,OB=10,
∴100=
OH,
∴OH=8,
∴BH=
=6.
∵DE∥AB,∠OBA=90°,
∴∠EFB=∠OBA=90°.
∵BE∥AD,
∴∠EBO=∠BOA,
∴△BFE∽△OHB,
∴
=
,
∴
=
,
解得:t=
,
∴EB=
×
=
,
∴S?ABED=
×6=
,
∴E点运动
秒时,四边形ABED是平行四边形,此时该平行四边形的面积为
.
(2)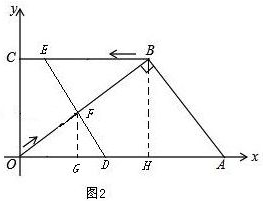 过点F作FG⊥OA于G,如图2,
过点F作FG⊥OA于G,如图2,
则有FG∥BH,
∴△OGF∽△OHB,
∴
=
=
,
∴
=
=
,
∴OG=2t,GF=
,
∴点F(2t,
t).
∵BC=OH=8,BE=
t,
∴CE=8-
t,
∴点E(8-
t,6).
若点E、F都在反比例函数y=
上,
则有k=6(8-
t)=2t×
t,
解得:
(舍去),
,
∴当动点E、F运动的时间为1秒时,点E、F都在反比例函数y=
的图象上.
则有BE=
| 15 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
∵∠OBA=90°,
∴∠OHB=∠OBA.
又∵∠BOH=∠AOB,
∴△OHB∽△OBA,
∴
| OB |
| OA |
| OH |
| OB |

∴OB2=OH•OA.
∵A(
| 25 |
| 2 |
| 25 |
| 2 |
∴100=
| 25 |
| 2 |
∴OH=8,
∴BH=
| OB2-OH2 |
∵DE∥AB,∠OBA=90°,
∴∠EFB=∠OBA=90°.
∵BE∥AD,
∴∠EBO=∠BOA,
∴△BFE∽△OHB,
∴
| BF |
| OH |
| BE |
| OB |
∴
10-
| ||
| 8 |
| ||
| 10 |
解得:t=
| 20 |
| 17 |
∴EB=
| 15 |
| 2 |
| 20 |
| 17 |
| 150 |
| 17 |
∴S?ABED=
| 150 |
| 17 |
| 900 |
| 17 |
∴E点运动
| 20 |
| 17 |
| 900 |
| 17 |
(2)
 过点F作FG⊥OA于G,如图2,
过点F作FG⊥OA于G,如图2,则有FG∥BH,
∴△OGF∽△OHB,
∴
| OG |
| OH |
| GF |
| HB |
| OF |
| OB |
∴
| OG |
| 8 |
| GF |
| 6 |
| ||
| 10 |
∴OG=2t,GF=
| 3t |
| 2 |
∴点F(2t,
| 3 |
| 2 |
∵BC=OH=8,BE=
| 15 |
| 2 |
∴CE=8-
| 15 |
| 2 |
∴点E(8-
| 15 |
| 2 |
若点E、F都在反比例函数y=
| k |
| x |
则有k=6(8-
| 15 |
| 2 |
| 3 |
| 2 |
解得:
|
|
∴当动点E、F运动的时间为1秒时,点E、F都在反比例函数y=
| 3 |
| x |
点评:本题主要考查了相似三角形的判定与性质、平行四边形的性质、运用待定系数法求反比例函数的解析式等知识,求出点E、F的坐标(用t表示)是解决第(2)小题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在Rt△ABC中,∠C=90°,AB=3,AC=2,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
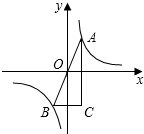 如图,A,B是函数y=
如图,A,B是函数y= 如图所示,图中有
如图所示,图中有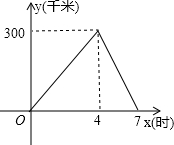 小李从甲地前往乙地,到达乙地后立刻返回,他与甲地的距离y(千米)与所用时间x(时)的函数关系如图所示.
小李从甲地前往乙地,到达乙地后立刻返回,他与甲地的距离y(千米)与所用时间x(时)的函数关系如图所示.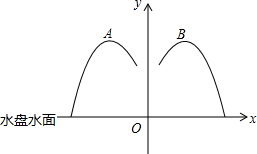 一个台型喷泉,若沿着中轴线截面,得到如图所示的抛物线,一个单位长度是1米,已知这两段抛物线关于y轴对称,其右侧的抛物线为:
一个台型喷泉,若沿着中轴线截面,得到如图所示的抛物线,一个单位长度是1米,已知这两段抛物线关于y轴对称,其右侧的抛物线为: