题目内容
3.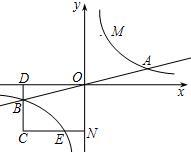 已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点,第一象限上的点M(m,n)(在A点左侧)是双曲线的动点,过点B作BD∥于y轴于点D,过N(-,-n)作NC∥x轴交双曲线于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为y=$\frac{2}{3}$x+$\frac{2}{3}$.
已知双曲线y=$\frac{k}{x}$与直线y=$\frac{1}{4}$x相交于A、B两点,第一象限上的点M(m,n)(在A点左侧)是双曲线的动点,过点B作BD∥于y轴于点D,过N(-,-n)作NC∥x轴交双曲线于点E,交BD于点C.若B是CD的中点,四边形OBCE的面积为4,则直线CM的解析式为y=$\frac{2}{3}$x+$\frac{2}{3}$.
分析 根据一次函数和反比例函数的性质及点的坐标和解析式的关系解答.
解答 解:设B点坐标为(x1,-$\frac{n}{2}$),代入y=$\frac{1}{4}$x得,-$\frac{n}{2}$=$\frac{1}{4}$x1,x1=-2n;
∴B点坐标为(-2n,-$\frac{n}{2}$).
因为BD∥y轴,所以C点坐标为(-2n,-n).
因为四边形ODCN的面积为2n•n=2n2,三角形ODB,三角形OEN的面积均为$\frac{k}{2}$,四边形OBCE的面积为4.
则有2n2-k=4---①;
又因为2n•$\frac{n}{2}$=k,即n2=k---②
②代入①得,4=2k-k,解得k=4;则解析式为y=$\frac{4}{x}$;
又因为n2=4,故n=2或n=-2.
M在第一象限,n>0;
将M(m,2)代入解析式y=$\frac{4}{x}$,得m=2.故M点坐标为(2,2);C(-4,-2);
设直线CM解析式为y=kx+b,则$\left\{\begin{array}{l}{2k+b=2}\\{-4k+b=-2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{2}{3}}\\{b=\frac{2}{3}}\end{array}\right.$
∴一次函数解析式为:y=$\frac{2}{3}$x+$\frac{2}{3}$.
故答案为:y=$\frac{2}{3}$x+$\frac{2}{3}$.
点评 此题主要考查了待定系数法函数解析式以及一次函数与反比例函数交点的性质,根据四边形OBCE的面积为4得出k的值是解决问题的关键.

练习册系列答案
相关题目
13.一个数的平方根等于它本身的数是( )
| A. | -1 | B. | 0 | C. | ±1 | D. | ±1或0 |
11. 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
 将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )
将宽为$\sqrt{3}$cm的长方形纸条折叠成如图所示的形状,则折痕PQ的长是( )| A. | 1cm | B. | 2cm | C. | $\frac{\sqrt{6}}{2}$cm | D. | $\sqrt{3}$cm |
18.下面各对数中互为相反数的是( )
| A. | (-3)2与-32 | B. | (-2)3与-23 | C. | -22与32 | D. | (-3×2)2与-3×22 |
15.实数$\root{3}{-64}$、2$\frac{1}{4}$、$\frac{25}{3}$、$\frac{π}{2}$、3.14、$\sqrt{3}$、$\sqrt{64}$、0$\stackrel{•}{4}$中,无理数有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
12.某同学想了解2016年10月国庆节期间某一天,新泰市青云路与向阳路交叉路口1分钟内各个方向通行的车辆数量,他应采取的收集数据方法为( )
| A. | 查阅资料 | B. | 实验 | C. | 问卷调查 | D. | 观察 |
14.如图是一数值转换机的示意图,则输出结果是( )


| A. | 3x2-$\frac{1}{2}$ | B. | $\frac{(3x)^{2}-1}{2}$ | C. | $\frac{3{x}^{2}-1}{2}$ | D. | $\frac{(3x-1)^{2}}{2}$ |