题目内容
10. 已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE.
已知:点A、C分别是∠B的两条边上的点,点D、E分别是直线BA、BC上的点,直线AE、CD相交于点P点,D、E分别在线段BA、BC上.若∠B=60°,且AD=BE,BD=CE.(1)求证△ABC是等边三角形
(2)判断△AEC≌△BCD吗?若全等请说明理由.
(3)求∠APD的度数.
分析 (1)利用等式的性质得出AB=BC,即可得出结论;
(2)由(1)知△ABC是等边三角形,由等边三角形的性质就可以得出△CBD≌△ACE
(3)由(2)△CBD≌△ACE就可以得出∠BCD=∠CAE,就可以得出结论;
解答 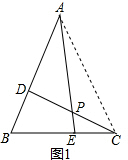 解:(1)如图,连结AC,
解:(1)如图,连结AC,
∵AD=BE,BD=CE,
∴AD+BD=BE+CE,
∴AB=BC.
∵∠B=60°,
∴△ABC为等边三角形.
(2)△AEC≌△BCD,
理由:由(1)知,△ABC为等边三角形.
∴∠B=∠ACB=60°,BC=AC.
在△CBD和△ACE中$\left\{\begin{array}{l}{BC=AC}\\{∠B=∠ACB}\\{BD=CE}\end{array}\right.$,
∴△CBD≌△ACE(SAS),
(3)由(2)知,△CBD≌△ACE
∴∠BCD=∠CAE.
∵∠APD=∠CAE+∠ACD,
∴∠APD=∠BCD+∠ACD=60°.
点评 此题是三角形综合题,主要考查了全等三角形的判定与性质的运用,等边三角形的判定及性质的运用,解答时证明三角形全等是关键.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
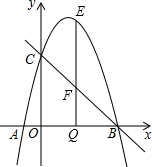 如图,直线y=-x+3与x轴交于B点,与y轴交于点C,抛物线y=-x2+bx+c经过B、C两点,且与x轴交于另一点A(A在B的左边).
如图,直线y=-x+3与x轴交于B点,与y轴交于点C,抛物线y=-x2+bx+c经过B、C两点,且与x轴交于另一点A(A在B的左边). 如图,直线y=$\frac{1}{2}x$-2和双曲线y=$\frac{k}{x}$相交于A(b,1),点P在直线y=$\frac{1}{2}$x-2上,且P点的纵坐标为-1,过P作PQ∥y轴交双曲线于点Q.
如图,直线y=$\frac{1}{2}x$-2和双曲线y=$\frac{k}{x}$相交于A(b,1),点P在直线y=$\frac{1}{2}$x-2上,且P点的纵坐标为-1,过P作PQ∥y轴交双曲线于点Q.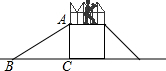 如图为某公园(六•一)前新增设的一台滑梯截面,已知该滑梯高度AC=2m,滑梯着地点B与梯架之间的距离BC=4m.
如图为某公园(六•一)前新增设的一台滑梯截面,已知该滑梯高度AC=2m,滑梯着地点B与梯架之间的距离BC=4m. 已知:如图,在△ABC中,DE∥BC,EF∥DC
已知:如图,在△ABC中,DE∥BC,EF∥DC 如图,△ABC中,AD是中线,△ACD旋转后能与△EBD重合.
如图,△ABC中,AD是中线,△ACD旋转后能与△EBD重合.