题目内容
12. 如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2$\sqrt{3}$,那么AC的长等于6.
如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2$\sqrt{3}$,那么AC的长等于6.
分析 连接OB,则△AOB是直角三角形,利用三角函数即可求得OA的长,则AC即可求解.
解答  解:连接OB.
解:连接OB.
∵AB是⊙O的切线,B为切点,
∴OB⊥AB,
在直角△OAB中,OB=AB•tanA=2$\sqrt{3}$×$\frac{\sqrt{3}}{3}$=2,
则OA=2OB=4,
∴AC=4+2=6.
故答案是:6.
点评 本题考查了三角函数以及切线的性质,正确判断△OAB是直角三角形是关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
17.若x2=6x-2化为一元二次方程的一般形式后,二次项系数、一次项系数和常数项分别是( )
| A. | 1,6,-2 | B. | 1,-6,-2 | C. | 1,-6,2 | D. | 6,1,-2 |
2.将方程3x2+1=6x化为一元二次方程的一般形式后,其二次项系数和一次项系数分别为( )
| A. | -3,-6 | B. | 3,-6 | C. | -3,-6 | D. | 3,6 |
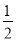 x2+2x+y-1=0,则x+2y的最大值为_________ .
x2+2x+y-1=0,则x+2y的最大值为_________ . 网上购物已经成为当今年轻人的一种潮流生活,同时也催生了快递行业的高速发展.在刚刚过去的2016年“双十一”活动大促销的当天,小明欲购买一部分商品,经了解有甲、乙两家快递公司分别给出了快递费y(元)与物品重量x(千克)之间的函数图象,根据图象中的有关数据解答下列问题:
网上购物已经成为当今年轻人的一种潮流生活,同时也催生了快递行业的高速发展.在刚刚过去的2016年“双十一”活动大促销的当天,小明欲购买一部分商品,经了解有甲、乙两家快递公司分别给出了快递费y(元)与物品重量x(千克)之间的函数图象,根据图象中的有关数据解答下列问题: