题目内容
4. 网上购物已经成为当今年轻人的一种潮流生活,同时也催生了快递行业的高速发展.在刚刚过去的2016年“双十一”活动大促销的当天,小明欲购买一部分商品,经了解有甲、乙两家快递公司分别给出了快递费y(元)与物品重量x(千克)之间的函数图象,根据图象中的有关数据解答下列问题:
网上购物已经成为当今年轻人的一种潮流生活,同时也催生了快递行业的高速发展.在刚刚过去的2016年“双十一”活动大促销的当天,小明欲购买一部分商品,经了解有甲、乙两家快递公司分别给出了快递费y(元)与物品重量x(千克)之间的函数图象,根据图象中的有关数据解答下列问题:(1)请求出乙快递公司快递费用y(元)与x(千克)之间的函数关系式;
(2)当物品的重量x(千克)在哪个范围时,选择乙快递公司更划算?
分析 (1)设乙快递公司快递费用y(元)与x(千克)之间的函数关系式为y乙=kx+b(k≠0),根据图象中点的坐标利用待定系数法即可求出该函数关系式;
(2)设在0≤x≤2段,甲快递公司快递费用y(元)与x(千克)之间的函数关系式为y甲=mx(m≠0),利用待定系数法求出该取值范围内的函数关系式,令y甲=y乙求出x值,再结合函数图象的上下位置关系即可得出结论.
解答 解:(1)设乙快递公司快递费用y(元)与x(千克)之间的函数关系式为y乙=kx+b(k≠0),
将(0,2)、(4,38)代入y乙=kx+b中,
$\left\{\begin{array}{l}{b=2}\\{4k+b=38}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=9}\\{b=2}\end{array}\right.$,
∴乙快递公司快递费用y(元)与x(千克)之间的函数关系式为y乙=9x+2.
(2)设在0≤x≤2段,甲快递公司快递费用y(元)与x(千克)之间的函数关系式为y甲=mx(m≠0),
将(2,24)代入y甲=mx中,
24=2m,解得:m=12,
∴甲快递公司快递费用y(元)与x(千克)之间的函数关系式为y甲=12x(0≤x≤2).
在0≤x≤2段,令y甲=y乙,即9x+2=12x,
解得:x=$\frac{2}{3}$.
结合图形即可得出:当$\frac{2}{3}$<x<4时,选择乙快递公司更划算.
点评 本题考查了一次函数的应用,观察图形找出点的坐标再利用待定系数法求出函数解析式是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
15.a<0,b<0,|a|<|b|,则a,b大小关系是( )
| A. | a<b | B. | a>b | C. | a≥b | D. | a=b |
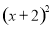 +
+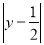 =0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。
=0,求5x2y—[2x2y-(xy2-2x2y)-4]-2xy2的值。 如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2$\sqrt{3}$,那么AC的长等于6.
如图,AB是⊙O的切线,B为切点,AO的延长线交⊙O于C点,连接BC,如果∠A=30°,AB=2$\sqrt{3}$,那么AC的长等于6. 如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm.
如图,形如量角器的半圆O的直径DE=12cm,形如三角板的△ABC中,∠ACB=90°,∠ABC=30°,BC=12cm半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上.设运动时间为t(s),当t=0s时,半圆O在△ABC的左侧,OC=8cm. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论: 在湖中三座小岛上建立了如图所示的两座桥,桥AB与桥CD平行,若∠ABC=120°,则∠BCD=120°.
在湖中三座小岛上建立了如图所示的两座桥,桥AB与桥CD平行,若∠ABC=120°,则∠BCD=120°.