题目内容
7.某中学新建了一栋4层的教学大楼,每层楼有8间教室,进出这栋大楼共有4道门,其中两道正门大小相同,两道侧门大小也相同.安全检查中,对4道门进行了测试:当同时开启一道正门和两道侧门时,2分钟内可以通过560名学生;当同时开启一道正门和一道侧门时,4分钟内可以通过800名学生.(1)求平均每分钟一道正门和一道侧门各可以通过多少名学生?
(2)检查中发现,紧急情况下因学生拥挤,出门的效率将降低10%,安全检查规定,在紧急情况下,全大楼的学生应在4分钟内通过这4道门安全撤离,问:这栋教学楼平均每间教室最多多少人?
分析 (1)设平均每分钟一道正门可通过x名学生,一道侧门可以通过y名学生,根据:2分钟内通过一道正门和两道侧门的人数为560,4分钟内通过一道正门和一道侧门的人数为800,列出方程组,解方程组可得;
(2)由题意知一道正门可通过的学生为120×0.9,一道侧门可通过的人数为80×0.9,根据4道门4分钟通过的人数不小于教学楼内总人数列出不等式,解不等式可得.
解答 解:(1)设平均每分钟一道正门可通过x名学生,一道侧门可以通过y名学生,
根据题意得:$\left\{\begin{array}{l}{2(x+2y)=280}\\{4(x+y)=800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=120}\\{y=80}\end{array}\right.$.
答:平均每分钟一道正门可通过120名学生,一道侧门可以通过80名学生;
(2)设每间教室可容纳m人,根据题意,
得:4(120×0.9×2+80×0.9×2)≥32x,
解得:x≤45.
答:这栋教学楼平均每间教室最多45人.
点评 本题考查了二元一次方程组及不等式的应用,解题关键是根据题意找出合适的等量关系或不等关系,再求解.

练习册系列答案
相关题目
 如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE交CD于F点,∠E=36°,求∠AFC的度数.
如图,?ABCD的顶点A、B、D在⊙O上,顶点C在⊙O的直径BE上,连接AE交CD于F点,∠E=36°,求∠AFC的度数.
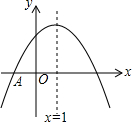 抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③-1≤a≤-$\frac{2}{3}$;④3≤n≤4中,正确的是①③.
抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①当x>3时,y<0;②3a+b>0;③-1≤a≤-$\frac{2}{3}$;④3≤n≤4中,正确的是①③.