题目内容
矩形ABCD的两条对角线AC、BD的长分别是关于x的一元二次方程（k-1）x2-6x+9=0的两根，则k= ．
考点：矩形的性质,根的判别式
专题：
分析：利用矩形的性质得出对角线相等，再利用根的判别式求出k的值．
解答：解：∵矩形ABCD的两条对角线AC、BD的长分别是关于x的一元二次方程（k-1）x2-6x+9=0的两根，
∴方程有两个相等的实数根，
∴b2-4ac=36-4×（k-1）×9=72-36k=0，
解得：k=2．
故答案为：2．
∴方程有两个相等的实数根，
∴b2-4ac=36-4×（k-1）×9=72-36k=0，
解得：k=2．
故答案为：2．
点评：此题主要考查了矩形的性质以及一元二次方程根的判别式等知识，熟练应用一元二次方程根的判别式是解题关键．
练习册系列答案
相关题目
如图，矩形ABCD中，AD=a，AB=b，依次连结它的各边中点得到第一个四边形E1F1G1H1，再依次连结四边形E1F1G1H1的各边中点得到第二个四边形E2F2G2H2，按此方法继续下去，得到的第n个四边形EnFnGnHn的面积等于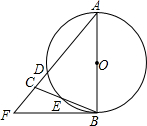
如图，在△ABC中，AB=AC=10，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF=