题目内容
20.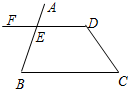 如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.
如图,已知∠C+∠D=180°,则∠AED=∠B.完成下面的说理过程.解:已知∠C+∠D=180°,
根据(同旁内角互补,两直线平行),
得DF∥BC,
又根据(两直线平行,同位角相等),
得∠AED=∠B.
分析 根据平行线的判定方法可判定DF∥BC,再由平行线的性质可得到∠AED=∠B,据此填空即可.
解答 解:已知∠C+∠D=180°,
根据( 同旁内角互补,两直线平行),
得DF∥BC,
又根据( 两直线平行,同位角相等),
得∠AED=∠B.
故答案为:同旁内角互补,两直线平行;BC;两直线平行,同位角相等.
点评 本题主要考查平行线的判定和性质,掌握平行线的判定和性质是解题的关键,即①同位角相等?两直线平行,②内错角相等?两直线平行,③同旁内角互补?两直线平行,④a∥b,b∥c⇒a∥c.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.在平面直角坐标系中,点O是坐标原点,点A是x轴正半轴上的一个定点,点B是反比例函数y=$\frac{k-3}{x}$(y>0)的图象上一个动点,当△ABO的面积随点B的横坐标增大而减小时,则k的取值范围是( )
| A. | k<3 | B. | k≤3 | C. | k>3 | D. | k≥3 |
15. 如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
 如图,射线AB、AC被直线DE所截,则∠1与∠2是( )
如图,射线AB、AC被直线DE所截,则∠1与∠2是( )| A. | 同位角 | B. | 内错角 | C. | 同旁内角 | D. | 对顶角 |
5.下列说法不正确的是( )
| A. | 全等三角形的对应边相等,对应角相等 | |
| B. | 全等三角形的对应边上的中线相等 | |
| C. | 两条边和一个角对应相等的两个三角形全等 | |
| D. | 全等三角形的面积相等 |
12.若$a=\sqrt{7}-2\sqrt{2}$,则${a^2}+\frac{1}{a^2}+2$=( )
| A. | 16 | B. | 32 | C. | -16 | D. | -32 |
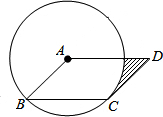 如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,已知半径AB=2,则图中阴影部分面积为(2-$\frac{π}{2}$)cm2.
如图,在?ABCD中,以点A为圆心,AB的长为半径的圆恰好与CD相切于点C,交AD于点E,已知半径AB=2,则图中阴影部分面积为(2-$\frac{π}{2}$)cm2. 如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )
如图,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,连接EF、CF,则下列结论中一定成立的是( )