题目内容
4.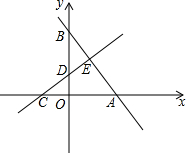 如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、点B,直线CD与x轴、y轴分别交于点C、点D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=$\frac{3}{4}$.
如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A、点B,直线CD与x轴、y轴分别交于点C、点D,AB与CD相交于点E,线段OA,OC的长是一元二次方程x2-18x+72=0的两根(OA>OC),BE=5,tan∠ABO=$\frac{3}{4}$.(1)求点A、点C、点E的坐标;
(2)求sin∠DCO的值;
(3)在x轴上是否存在一点P,使以点C、点E、点P为顶点的三角形与△DCO相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
分析 (1)首先解方程x2-18x+72=0求得方程的根,则A和C的坐标即可求得,然后根据三角函数求得B的坐标,作EF⊥x轴于点F,根据△AEF∽△ABO,利用相似三角形的性质求得EF和OF的长,即可求得E的坐标;
(2)求得直线CD的解析式,则D的坐标即可求得,然后根据三角函数的定义求解;
(3)设P的坐标是(p,0),则PC=p+6.分成△COD∽△CEP和△COD∽△CPE两种情况进行讨论即可求解.
解答 解:(1)x2-18x+72=0即(x-12)(x-6)=0,
则x-12=0,x-6=0,
解得:x=12或x=6,
又∵OA>OC,
∴OA=12,OC=6,
∴A的坐标是(12,0),C的坐标是(-6,0).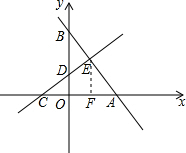
∵tan∠ABO=$\frac{OA}{OB}$=$\frac{3}{4}$,
∴OB=$\frac{4}{3}$OA=16,
则B的坐标是(0,16).AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{1{2}^{2}+1{6}^{2}}$=20.
作EF⊥x轴于点F.
则△AEF∽△ABO,
∴$\frac{AF}{OA}=\frac{EF}{OB}=\frac{AE}{BE}$=$\frac{15}{20}$=$\frac{3}{4}$,
∴$\frac{AF}{12}=\frac{EF}{16}$=$\frac{3}{4}$,
∴AF=9,EF=12,
则OF=12-9=3,
则E的坐标是(3,12);
(2)设直线CD的解析式是y=kx+b,则$\left\{\begin{array}{l}{-6k+b=0}\\{3k+b=12}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=8}\end{array}\right.$,
则直线CD的解析式是y=-$\frac{4}{3}$x+8,
令x=0,则y=8,则D的坐标是(0,8),OD=8.
则在直角△OCD中,CD=$\sqrt{O{C}^{2}+O{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
则sin∠DCO=$\frac{OD}{CD}$=$\frac{8}{10}$=$\frac{4}{5}$;
(3)设P的坐标是(p,0),则PC=p+6.
当△COD∽△CEP时,$\frac{CD}{CP}=\frac{OC}{CE}$,即$\frac{10}{p+6}=\frac{6}{15}$,
解得:d=19,
则P的坐标是(19,0);
当△COD∽△CPE时,$\frac{OC}{CP}=\frac{CD}{CE}$,则$\frac{6}{p+6}=\frac{10}{15}$,
解得:p=3,
则P的坐标是(3,0).
总之,P的坐标是(19,0)和(3,0).
点评 本题考查了待定系数法求函数的解析式以及相似三角形的判定与性质,正确求得E的坐标是解决本题的关键.

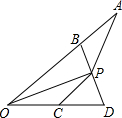 如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )
如图,OP平分∠AOD,B、C分别是OA、OD上的点,且OB≠OC,AB=CD,PC=AP,则下列结论中一定成立的个数有( )①S△ABP=S△PCD;②OP=BP;③∠AOD+∠APC=180°;④AO+OC=2OB.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
(1)①加工罐头的工人为(30-x)人,可以加工罐头300(30-x)千克;(用含x的式子表示)
②采摘水果的工人至少多少人?
(2)直接出售和加工罐头出售的利润如表:
| 销售方式 | 直接出售 | 加工成罐头销售 |
| 利润(元/千克) | 4 | 10 |
| A. | P不成立,则Q不成立 | B. | Q成立,则P成立 | ||
| C. | Q不成立,则P不成立 | D. | 以上三种说法均错误 |

