题目内容
18.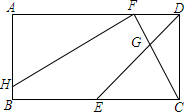 在矩形ABCD中,E为BC的中点,连接DE,F为AD上一点,连接CF,交DE于点G,过点F作HF⊥CF于点F,若$\frac{AB}{BC}=\frac{DG}{GE}$=$\frac{1}{2}$,DF=2.
在矩形ABCD中,E为BC的中点,连接DE,F为AD上一点,连接CF,交DE于点G,过点F作HF⊥CF于点F,若$\frac{AB}{BC}=\frac{DG}{GE}$=$\frac{1}{2}$,DF=2.(1)求证:2DF=CE;
(2)试判断∠FDE与∠EDC之间的数量关系,并说明理由;
(3)求HB的长度.
分析 (1)根据矩形的性质得到AD∥BC,推出△DFG∽△CEG,根据相似三角形的性质即可得到结论.
(2)根据矩形的性质得到∠DCB=90°,CD=AB,根据已知条件得到CE=$\frac{1}{2}$BC,于是得到CD=$\frac{1}{2}$BC,等量代换得到CD=CE,即可得到结论;
(3)根据(1)(2)的结论推出△AHF∽△CDF,由相似三角形的性质得到$\frac{AH}{AF}=\frac{DF}{CD}$=$\frac{1}{2}$,由DF=2,求得CD=AB=4,AD=8,即可求得结果.
解答 (1)证明:在矩形ABCD中,
∵AD∥BC,
∴△DFG∽△CEG,
∴$\frac{DF}{CE}=\frac{DG}{GE}$=$\frac{1}{2}$,
∴2DF=CE;
(2)∠FDE=∠EDC,
在矩形ABCD中,
∵∠DCB=90°,CD=AB,
∵E为BC的中点,
∴CE=$\frac{1}{2}$BC,
∵$\frac{AB}{BC}$=$\frac{1}{2}$,
∴CD=$\frac{1}{2}$BC,
∴CD=CE,
∴∠FDE=∠EDC;
(3)∵2DF=CE,
∴$\frac{DF}{CD}=\frac{1}{2}$,
∵∠A=∠CDF=90°,
∵HF⊥CF,
∴∠HFC=90°,
∴∠AFH+∠AHF=∠AFH+∠CFD=90°,
∴∠AHF=∠DFC,
∴△AHF∽△CDF,
∴$\frac{AH}{AF}=\frac{DF}{CD}$=$\frac{1}{2}$,
∵DF=2,
∴CD=AB=4,AD=8,
∴AF=6,
∴AH=3,
∴BH=1.
点评 本题考查了相似三角形的判定和性质,矩形的性质,等腰直角三角形的判定和性质,熟练掌握相似三角形的判定和性质是解题的关键.

| A. | +(-5)和-(+5) | B. | a与-a | C. | π与-3.14 | D. | -(-2.7)与2.7 |
| A. | 相等的角是对顶角 | |
| B. | 三角形的一个外角等于两个内角之和 | |
| C. | 如果a3=b3,那么a=b | |
| D. | 内错角相等 |
| A. | ①②③④ | B. | ①②③ | C. | ①②④ | D. | ①②③④ |
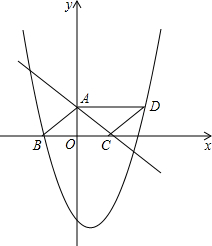 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B、点D在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且四边形ABCD是平行四边形.