题目内容
13. 如图,矩形ABCD中,AD=2AB
如图,矩形ABCD中,AD=2AB(1)作边BC的垂直平分线,交AD于点E,交BC于点F;(用尺规作图,不用写作法,但要保留作图痕迹)
(2)在(1)中,证明:四边形ABFE是正方形.
分析 (1)利用线段垂直平分线的作法得出即可;
(2)利用正方形的判定方法,一组邻边相等的矩形是正方形进而得出.
解答 (1)解:如图所示: ;
;
(2)证明:由题意可得:∠A=∠B=∠BFE=90°,
故四边形ABFE是矩形,
∵AD=2AB,BF=FC,
∴AB=BF,
∴矩形ABFE是正方形.
点评 此题主要考查了正方形的判定以及线段垂直平分线的作法,正确把握线段垂直平分线的性质是解题关键.

练习册系列答案
相关题目
4.正六边形的半径是6,则这个正六边形的面积为( )
| A. | 24 | B. | 54 | C. | 9$\sqrt{3}$ | D. | 54$\sqrt{3}$ |
18.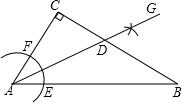 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
 如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:
如图,在△ABC中,∠C=90°,∠CAB=50°,按以下步骤作图:①以点A为圆心,小于AC长为半径画弧,分别交AB、AC于点E、F;
②分别以点E、F为圆心,大于$\frac{1}{2}$EF长为半径画弧,两弧相交于点G;
③作射线AG,交BC边于点D.
则∠ADC的度数为( )
| A. | 40° | B. | 55° | C. | 65° | D. | 75° |
5.计算:3x3•x等于( )
| A. | 3 | B. | 3x3 | C. | 3x4 | D. | 3x3 |
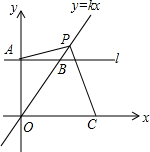 如图,直线l∥x轴,交y轴于点A(0,2),交直线y=kx(k>0)于点B,点P是线段OB延长线上一定,连接AP,过点P作PC⊥AP交x轴于点C.
如图,直线l∥x轴,交y轴于点A(0,2),交直线y=kx(k>0)于点B,点P是线段OB延长线上一定,连接AP,过点P作PC⊥AP交x轴于点C.