题目内容
10.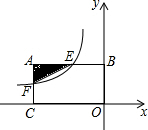 如图,矩形ABOC的边OC、OB分别在x轴负半轴、y轴正半轴上,反比例函数的图象经过AB的中点E,交AC于点F,连结EF.若△AEF的面积为$\frac{3}{2}$,则反比例函数的解析式为:y=-$\frac{3}{x}$.
如图,矩形ABOC的边OC、OB分别在x轴负半轴、y轴正半轴上,反比例函数的图象经过AB的中点E,交AC于点F,连结EF.若△AEF的面积为$\frac{3}{2}$,则反比例函数的解析式为:y=-$\frac{3}{x}$.
分析 设反比例函数的解析式为y=$\frac{k}{x}$,A(a,b),根据已知条件得到E($\frac{1}{2}$a,b),F(a,$\frac{k}{a}$),根据△AEF的面积为$\frac{3}{2}$,列方程$\frac{1}{2}$AE•AF=$\frac{1}{2}×(-\frac{1}{2}a)(b-\frac{k}{a})$=$\frac{3}{2}$,即可得到结论.
解答 解:设反比例函数的解析式为:y=$\frac{k}{x}$,A(a,b),
∵四边形ABCO是矩形,E是AB的中点,
∴E($\frac{1}{2}$a,b),F(a,$\frac{k}{a}$),
∵△AEF的面积为$\frac{3}{2}$,
∴$\frac{1}{2}$AE•AF=$\frac{1}{2}×(-\frac{1}{2}a)(b-\frac{k}{a})$=$\frac{3}{2}$,
∴-$\frac{1}{4}$ab+$\frac{k}{4}$=$\frac{3}{2}$,
∵反比例函数的图象经过AB的中点E,
∴$\frac{1}{2}$ab=k,
∴k=-3,
∴反比例函数的解析式为:y=-$\frac{3}{x}$,
故答案为:y=-$\frac{3}{x}$.
点评 本题考查了反比例函数y=$\frac{k}{x}$(k≠0)系数k的几何意义:从反比例函数y=kx(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.

练习册系列答案
相关题目
5.下列图案是中心对称图形的共有( )个


| A. | 1 | B. | 2 | C. | 3 | D. | 4 |

 已知,如图,在△ABC中,点D,E分别在AB和BC上,DE的延长线交AC的延长线于点F,且BD=CF,DE=EF.
已知,如图,在△ABC中,点D,E分别在AB和BC上,DE的延长线交AC的延长线于点F,且BD=CF,DE=EF.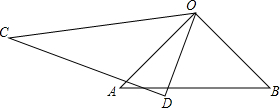 如图是一副三角板重叠而成的图形.其中∠AOB和∠CDO是直角,∠COD=60°,求∠AOD+△BOC的度数.
如图是一副三角板重叠而成的图形.其中∠AOB和∠CDO是直角,∠COD=60°,求∠AOD+△BOC的度数.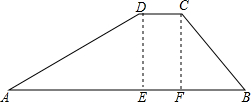 如图,水库大坝的横截面是梯形,坝顶CD宽是5m,坝高DE为20m,斜坡AD的坡度为1:$\sqrt{3}$,斜坡CB的坡度为5:6,建造这样的大坝1000m需要多少m3的土?(结果保留根号)
如图,水库大坝的横截面是梯形,坝顶CD宽是5m,坝高DE为20m,斜坡AD的坡度为1:$\sqrt{3}$,斜坡CB的坡度为5:6,建造这样的大坝1000m需要多少m3的土?(结果保留根号)