题目内容
设a、b、c是三角形的三边，x=ac-2bc，y=c2-bc，试比较x、y的大小．
考点：因式分解的应用,三角形三边关系
专题：
分析：比较两个代数式的大小即可求得两数的差，大于0可得到前者大，小于0可以得到后者大．
解答：解：∵x=ac-2bc，y=c2-bc，
∴x-y=ac-2bc-（c2-bc）=ac-bc-c2=c（a-b-c），
∵a、b、c是三角形的三边，
∴c＞0，a-b-c＜0，
∴x-y=c（a-b-c）＜0，
∴x＜y．
∴x-y=ac-2bc-（c2-bc）=ac-bc-c2=c（a-b-c），
∵a、b、c是三角形的三边，
∴c＞0，a-b-c＜0，
∴x-y=c（a-b-c）＜0，
∴x＜y．
点评：本题考查了因式分解的应用及三角形的三边关系，解题的关键是知道比较两个代数式的大小时可以通过求二者的差来完成，难度中等．
练习册系列答案
名校课堂系列答案
相关题目
二次函数y=a（x-h）2的图象如图，已知a=
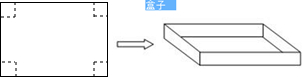如图，在一张长为acm，宽为bcm（a＞b＞2）的长方形纸片上的四个角处各剪去一个边长为1cm的小正方形，然后做成一个无盖的长方形的盒子，
如图，△ABC中，AB=6，BC=9，AC=11，E是AB上一点，且AE=4，在AC上求一点F，使A，E，F为顶点的三角形与以A，B，C为顶点的三角形相似．
在平面直角坐标系xOy中，A（0，4），B（2，0），C（5，1），D（2，5）．