题目内容
15．计算-（$\sqrt{2}$）2+（$\sqrt{2}$+π）0+（-$\frac{1}{2}$）-2的结果是（ ）| A． | 1 | B． | 2 | C． | $\frac{11}{4}$ | D． | 3 |
分析 首先计算乘方，然后从左向右依次计算，求出算式的值是多少即可．
解答 解：-（$\sqrt{2}$）2+（$\sqrt{2}$+π）0+（-$\frac{1}{2}$）-2
=-2+1+4
=3
故选：D．
点评 此题主要考查了实数的运算，要熟练掌握，解答此题的关键是要明确：在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．
练习册系列答案
相关题目
6．数学兴趣小组研究某型号冷柜温度的变化情况，发现该冷柜的工作过程是：当温度达到设定温度-20℃时，制冷停止，此后冷柜中的温度开始逐渐上升，当上升到-4℃时，制冷开始，温度开始逐渐下降，当冷柜自动制冷至-20℃时，制冷再次停止，…，按照以上方式循环进行．
同学们记录了44min内15个时间点冷柜中的温度y（℃）随时间x（min）的变化情况，制成下表：
（1）通过分析发现，冷柜中的温度y是时间x的函数．
①当4≤x＜20时，写出一个符合表中数据的函数解析式y=-$\frac{80}{x}$；
②当20≤x＜24时，写出一个符合表中数据的函数解析式y=-4x+76；
（2）a的值为-12；
（3）如图，在直角坐标系中，已描出了上表中部分数据对应的点，请描出剩余数据对应的点，并画出当4≤x≤44时温度y随时间x变化的函数图象．
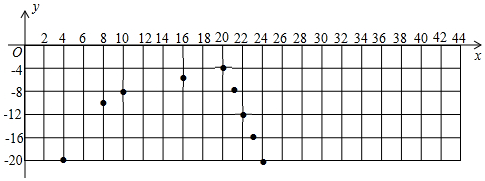
同学们记录了44min内15个时间点冷柜中的温度y（℃）随时间x（min）的变化情况，制成下表：
| 时间x/min | … | 4 | 8 | 10 | 16 | 20 | 21 | 22 | 23 | 24 | 28 | 30 | 36 | 40 | 42 | 44 | … |
| 温度y/℃ | … | -20 | -10 | -8 | -5 | -4 | -8 | -12 | -16 | -20 | -10 | -8 | -5 | -4 | a | -20 | … |
①当4≤x＜20时，写出一个符合表中数据的函数解析式y=-$\frac{80}{x}$；
②当20≤x＜24时，写出一个符合表中数据的函数解析式y=-4x+76；
（2）a的值为-12；
（3）如图，在直角坐标系中，已描出了上表中部分数据对应的点，请描出剩余数据对应的点，并画出当4≤x≤44时温度y随时间x变化的函数图象．
如图，直线l1∥l2，∠1=20°，则∠2+∠3=200°．
7．可燃冰，学名叫“天然气水合物”，是一种高效清洁、储量巨大的新能源．据报道，仅我国可燃冰预测远景资源量就超过了1000亿吨油当量．将1000亿用科学记数法可表示为（ ）
| A． | 1×103 | B． | 1000×108 | C． | 1×1011 | D． | 1×1014 |
4．
如图，几何体是由3个完全一样的正方体组成，它的左视图是（ ）
如图，几何体是由3个完全一样的正方体组成，它的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
10．“湖田十月清霜堕，晚稻初香蟹如虎”，在刚过去的十月是食蟹的好季节，某经销商去水产批发市场采购太湖蟹，他看中了A，B两家的某种品质相近的太湖蟹，零售价都为60元/千克，批发价各不相同．
A家规定：批发数量不超过100千克，按零售价的92%优惠；批发数量超过100千克但不超过200千克，按零售价的90%优惠；超过200千克的按零售价的88%优惠．
B家的规定如表：
（1）如果他批发90千克太湖蟹，则他在A，B两家批发分别需要多少元？
（2）如果他批发x千克太湖蟹（100＜x＜300），请你分别用含字母x的式子表示他在A，B两家批发所需的费用；
（3）现在他要批发185千克太湖蟹，你能帮助他选择在哪家批发更优惠吗？请说明理由．
A家规定：批发数量不超过100千克，按零售价的92%优惠；批发数量超过100千克但不超过200千克，按零售价的90%优惠；超过200千克的按零售价的88%优惠．
B家的规定如表：
| 数量范围（千克） | 0～50 部分（包括50） | 50以上～150 部分（包括150） | 150以上～250 部分（包括250） | 250以上 部分 |
| 价格（元） | 零售价的95% | 零售价的85% | 零售价的75% | 零售价的70% |
（2）如果他批发x千克太湖蟹（100＜x＜300），请你分别用含字母x的式子表示他在A，B两家批发所需的费用；
（3）现在他要批发185千克太湖蟹，你能帮助他选择在哪家批发更优惠吗？请说明理由．