题目内容
17.若二次函数y=ax2-4x+c的图象开口向下,交y轴于负半轴,其中a、c为整数,请写出一个符合条件的解析式y=-x2-4x-3.分析 根据二次函数图象的性质解答.
解答 解:∵二次函数y=ax2-4x+c的图象开口向下,交y轴于负半轴,其中a、c为整数,
∴a<0,c<0
∴y=-x2-4x-3(答案不唯一),
故答案为:y=-x2-4x-3.
点评 本题是开放型题目,主要考查二次函数图象的性质,只要符合要求即可.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
6.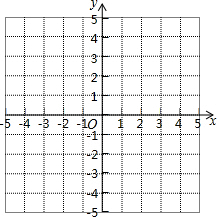 (1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
(1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
列表:
描点并连线.
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=-$\frac{6}{x}$(x<0)随之变大.
 (1)画出函数y=-$\frac{6}{x}$(x<0)的图象:
(1)画出函数y=-$\frac{6}{x}$(x<0)的图象:列表:
| x | … | -6 | -5 | -4 | -3 | -2 | -1 | … |
| y | … | … |
(2)从图象可以看出,曲线从左向右依次升高,当x由小变大时,y=-$\frac{6}{x}$(x<0)随之变大.
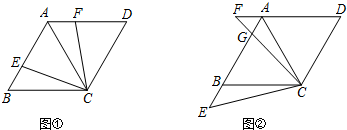
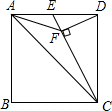 如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论:
如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论: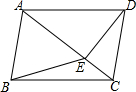 如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
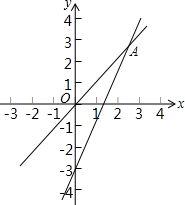 已知一个正比例函数与一个一次函数的图象交于点A(3,4),且0A=0B
已知一个正比例函数与一个一次函数的图象交于点A(3,4),且0A=0B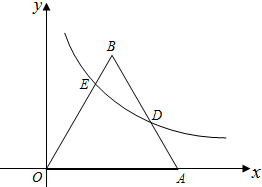 如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.
如图,等边△ABO在平面直角坐标系中,点A的坐标为(4,0),函数y=$\frac{k}{x}$(x>0,k是常数)的图象经过AB边的中点D,交OB边于点E.