题目内容
尺规作图:任意画一条线段线段,然后将其七等分.
考点:平行线分线段成比例,作图—复杂作图
专题:作图题
分析:从线段AB的端点A引射线AO,在射线AO上依次截取七段相等的线段,连接BK,再过AK的分点分别作BK的平行线,这些平行线于AB的交点就是线段AB的七等分点,可以根据平行线分线段成比例定理进行证明.
解答: 解:从线段AB的端点A引射线AO,在射线AO上依次截取AM=MN=NP=PH=HQ=QG=GK,
解:从线段AB的端点A引射线AO,在射线AO上依次截取AM=MN=NP=PH=HQ=QG=GK,
连接KB,过点M、N、P、H、Q、G分别作KB的平行线,分别交AB于H、C、D、E、F、G,
则点H、C、D、E、F、G为线段AB的七等份点.
 解:从线段AB的端点A引射线AO,在射线AO上依次截取AM=MN=NP=PH=HQ=QG=GK,
解:从线段AB的端点A引射线AO,在射线AO上依次截取AM=MN=NP=PH=HQ=QG=GK,连接KB,过点M、N、P、H、Q、G分别作KB的平行线,分别交AB于H、C、D、E、F、G,
则点H、C、D、E、F、G为线段AB的七等份点.
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
某钢铁厂1月份生产某种钢材5万吨,3月份生产这种钢材7.2万吨,设平均每月增长的百分率为x,则根据题意可列方程为( )
| A、5(1+x)=7.2 |
| B、5(1+x2)=7.2 |
| C、5(1+x)2=7.2 |
| D、7.2(1+x)2=5 |
抛物线y=x2-2x-3与y轴交于A点,则点A的坐标是( )
| A、(-1,0) |
| B、(0,-3) |
| C、(0,3) |
| D、(3,0) |
 如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=
如图所示:点P为∠AOB内一点,分别作出P点关于OA、OB的对称点P1,P2,连接P1P2交OA于M,交OB于N,△PMN的周长为15cm,P1P2=
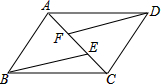 如图所示,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
如图所示,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.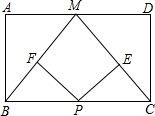 如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.
如图,点M是矩形ABCD边AD的中点,2AB=AD,点P是BC边上一动点,PE⊥MC,PF⊥BM,垂足分别为E、F,求点P运动到什么位置时,四边形PEMF为正方形,并证明.