Question

10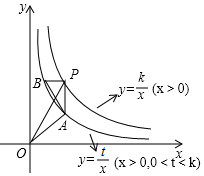．如图所示，Rt△PAB的直角顶点P（3，4）在函数y=$\frac{k}{x}$（x＞0）的图象上，顶点A、B在函数y=$\frac{t}{x}$（x＞0，0＜t＜k）的图象上，PA∥y轴，连接OP，OA，记△OPA的面积为S_△OPA，△PAB的面积为S_△PAB，设w=S_△OPA-S_△PAB．
①求k的值以及w关于t的表达式；   
②若用w_max和w_min分别表示函数w的最大值和最小值，令T=w_max+a²-a，其中a为实数，求T_min．

Answer 1

分析 （1）由点P的坐标表示出点A、点B的坐标，从而得S_△PAB=$\frac{1}{2}$•PA•PB=$\frac{1}{2}$（4-$\frac{t}{3}$）（3-$\frac{t}{4}$），再根据反比例系数k的几何意义知S_△OPA=S_△OPC-S_△OAC=6-$\frac{1}{2}$t，由w=S_△OPA-S_△PAB可得答案；
（2）将（1）中所得解析式配方求得w_max=$\frac{3}{2}$，代入T=w_max+a²-a配方即可得出答案．

解答 解：（1）∵点P（3，4），
∴在y=$\frac{t}{x}$中，当x=3时，y=$\frac{t}{3}$，即点A（3，$\frac{t}{3}$），
当y=4时，x=$\frac{t}{4}$，即点B（$\frac{t}{4}$，4），
则S_△PAB=$\frac{1}{2}$•PA•PB=$\frac{1}{2}$（4-$\frac{t}{3}$）（3-$\frac{t}{4}$），
如图，延长PA交x轴于点C，

则PC⊥x轴，
又S_△OPA=S_△OPC-S_△OAC=$\frac{1}{2}$×3×4-$\frac{1}{2}$t=6-$\frac{1}{2}$t，
∴w=6-$\frac{1}{2}$t-$\frac{1}{2}$（4-$\frac{t}{3}$）（3-$\frac{t}{4}$）=-$\frac{1}{24}$t²+$\frac{1}{2}$t；

（2）∵w=-$\frac{1}{24}$t²+$\frac{1}{2}$t=-$\frac{1}{24}$（t-6）²+$\frac{3}{2}$，
∴w_max=$\frac{3}{2}$，
则T=w_max+a²-a=a²-a+$\frac{3}{2}$=（a-$\frac{1}{2}$）²+$\frac{5}{4}$，
∴当a=$\frac{1}{2}$时，T_min=$\frac{5}{4}$．

点评 本题主要考查反比例函数系数k的几何意义及二次函数的性质，熟练掌握反比例系数k的几何意义及配方法求二次函数的最值是解题的关键．