题目内容
5. 如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).
如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b).(1)求b,m的值;
(2)垂直于x轴的直线x=a与直线l1,l2分别交于点C,D,若线段CD长为2,求a的值.
分析 (1)由点P(1,b)在直线l1上,利用一次函数图象上点的坐标特征,即可求出b值,再将点P的坐标代入直线l2中,即可求出m值;
(2)由点C、D的横坐标,即可得出点C、D的纵坐标,结合CD=2即可得出关于a的含绝对值符号的一元一次方程,解之即可得出结论.
解答 解:(1)∵点P(1,b)在直线l1:y=2x+1上,
∴b=2×1+1=3;
∵点P(1,3)在直线l2:y=mx+4上,
∴3=m+4,
∴m=-1.
(2)当x=a时,yC=2a+1;
当x=a时,yD=4-a.
∵CD=2,
∴|2a+1-(4-a)|=2,
解得:a=$\frac{1}{3}$或a=$\frac{5}{3}$.
∴a的值为$\frac{1}{3}$或$\frac{5}{3}$.
点评 本题考查了两条直线相交或平行问题、一次函数图象上点的坐标特征以及解含绝对值符号的一元一次方程,解题的关键是:(1)利用一次函数图象上点的坐标特征求出b、m的值;(2)根据CD=2,找出关于a的含绝对值符号的一元一次方程.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
13.小明化简(2x+1)(2x-1)-x(x+5)的过程如图,请指出他化简过程中的错误,写出对应的序号,并写出正确的化简过程.
| 解:原式=2x2-1-x(x+5)…① =2x2-1-x2+5x…② =x2+5x-1 …③ |
17.下列计算正确的是( )
| A. | 2x+3x=5x2 | B. | x2•x3=x6 | C. | (x2)3=x5 | D. | x5÷x3=x2 |
14.已知∠α和∠β的对顶角,若∠α=60°,则∠β的度数为( )
| A. | 30° | B. | 60° | C. | 70° | D. | 150° |
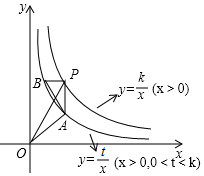 如图所示,Rt△PAB的直角顶点P(3,4)在函数y=$\frac{k}{x}$(x>0)的图象上,顶点A、B在函数y=$\frac{t}{x}$(x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA,△PAB的面积为S△PAB,设w=S△OPA-S△PAB.
如图所示,Rt△PAB的直角顶点P(3,4)在函数y=$\frac{k}{x}$(x>0)的图象上,顶点A、B在函数y=$\frac{t}{x}$(x>0,0<t<k)的图象上,PA∥y轴,连接OP,OA,记△OPA的面积为S△OPA,△PAB的面积为S△PAB,设w=S△OPA-S△PAB.