题目内容
18．半径为2的圆的内接正六边形的边长为2．分析 不妨设⊙O的内接正六边形为ABCDEF，连接OA、OB，则可证明△OAB为等边三角形，可求得边长．
解答 
解：
如图，⊙O的内接正六边形为ABCDEF，连接OA、OB，
∵六边形ABCDEF为正六边形，
∴∠AOB=$\frac{360°}{6}$=60°，
∴△AOB为等边三角形，
∴AB=OA=2，
故答案为：2．
点评 本题主要考查正多边形和圆，掌握正六边形的中心角为60°是解题的关键．
练习册系列答案
相关题目
13．
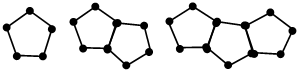用火柴棒按如图的方式搭五边形组成的图形
（1）填写表：
（2）照这样的规律搭下去，搭n个这样的五边形需要（4n+1）根火柴棒．
用火柴棒按如图的方式搭五边形组成的图形（1）填写表：
| 五边形个数 | 1 | 2 | 3 | 4 | 5 |
| 火柴棒根数 | 5 | 9 | 13 | 17 |