题目内容
7.若|4-x|+|1-x|+4的值恒为常数,x该满足的条件及此常数的值分别为1≤x≤4,7.分析 要使原式对任何数x恒为常数,则去掉绝对值符号,化简合并时,必须使含x的项相加为零,即x的系数之和为零.因此必须有|4-x|=4-x且|1-x|=x-1.让4-x≥0,x-1≥0列式计算即可求得x该满足的条件,进而化简代数式即可.
解答 解:x应满足的条件是:$\left\{\begin{array}{l}{4-x≥0}\\{x-1≥0}\end{array}\right.$,
解得1≤x≤4,
∴原式=4-x+x-1+4
=7,
故答案为1≤x≤4,7.
点评 本题考查了绝对值,代数式的化简及一元一次不等式组的应用;判断出绝对值内的代数式的符号是解决本题的关键;用到的知识点为:一个数的绝对值是非负数.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
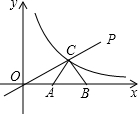 如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,△ABC是边长为3的等边三角形,且AB边在x轴额正半轴上,cos∠COA=$\frac{\sqrt{3}}{2}$.
如图,在平面直角坐标系中,正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$(m≠0)的图象在第一象限交于点C,△ABC是边长为3的等边三角形,且AB边在x轴额正半轴上,cos∠COA=$\frac{\sqrt{3}}{2}$. 如图所示,要建一个长方形的养鸡场,养鸡场的一边靠墙,如果用60m长的篱笆围成中间有一道篱笆的养鸡场,设养鸡场的长为xm,当x=30m时,养鸡场的面积最大.
如图所示,要建一个长方形的养鸡场,养鸡场的一边靠墙,如果用60m长的篱笆围成中间有一道篱笆的养鸡场,设养鸡场的长为xm,当x=30m时,养鸡场的面积最大.