题目内容
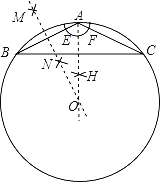
【题目】如图，在边长为4的正方形
中，点
为对角线
上一动点（点与点
、
不重合），连接
，作
交射线
于点
，过点作
分别交
，
于点
、
，作射线
交射线
于点
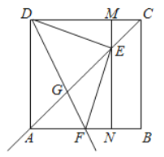
（1）求证：
；
（2）当
时，求
的长．
【答案】（1）见解析；（2）GE的长为
，
【解析】
（1）要证明EF＝DE，只要证明△DME≌△ENF即可，然后根据题目中的条件和正方形的性质，可以得到△DME≌△ENF的条件，从而可以证明结论成立；
（2）分两种情况：①当点F在线段AB上时，②当点F在BA的延长线上时；均可根据勾股定理和三角形相似，可以得到AG和CG、CE的长，然后即可得到GE的长．
（1）证明：∵四边形ABCD是正方形，AC是对角线，
∴∠ECM＝45°，
∵MN∥BC，∠BCM＝90°，
∴∠NMC＋∠BCM＝180°，∠MNB＋∠B＝180°，
∴∠NMC＝90°，∠MNB＝90°，
∴∠MEC＝∠MCE＝45°，∠DME＝∠ENF＝90°，
∴MC＝ME，
∵CD＝MN，
∴DM＝EN，
∵DE⊥EF，∠EDM＋∠DEM＝90°，
∵∠DEF＝90°，
∴∠DEM＋∠FEN＝90°，
∴∠EDM＝∠FEN，
在△DME和△ENF中
，
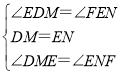∴△DME≌△ENF（ASA），
∴
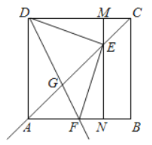
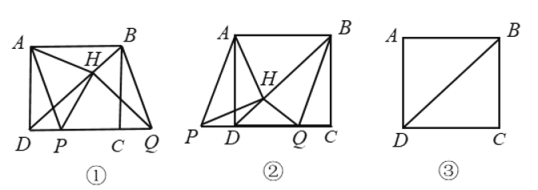
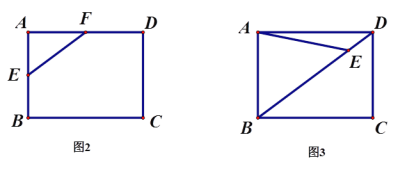
（2）如图1所示，由（1）知，△DME≌△ENF，
∴ME＝NF，
∵四边形MNBC是矩形，
∴MC＝BN，
又∵ME＝MC，AB＝4，AF＝2，
∴BN＝MC＝NF＝1，
∵∠EMC＝90°，
∴CE＝
，
∵AF∥CD，
∴△DGC∽△FGA，
∴
，
∴
，
∵AB＝BC＝4，∠B＝90°，
∴AC＝4，
∵AC＝AG＋GC，
∴AG＝
，CG＝
，
∴GE＝GCCE＝-=
；
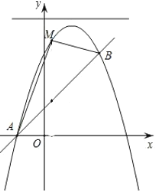
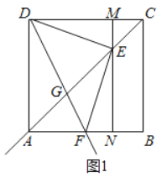
如图2所示，
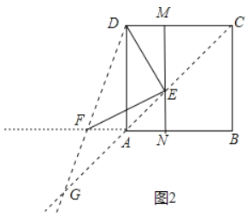
同理可得，FN＝BN，
∵AF＝2，AB＝4，
∴AN＝1，
∵AB＝BC＝4，∠B＝90°，
∴AC＝4，
∵AF∥CD，
∴△GAF∽△GCD，
∴，
即
，
解得，AG＝4，
∵AN＝NE＝1，∠ENA＝90°，
∴AE＝，
∴GE＝GA＋AE＝5．
