题目内容
如图是由9个等边三角形拼成的六边形，若中间的小等边三角形的边长是1，则六边形的周长是多少？考点：等边三角形的性质
专题：规律型
分析：设第二小的等边三角形的边长为x，而中间的小等边三角形的边长是1，根据等边三角形的三边都相等可得到其它等边三角形的边长分别x+1，x+2，x+3，并且x+3=2x，解得x=3，又这个六边形的周长=2x+2（x+1）+2（x+2）+x+3=7x+9，把x=3代入计算即可．
解答：解：如图，
设第二小的等边三角形的边长为x，而中间的小等边三角形的边长是1，
所以其它等边三角形的边长分别x+1，x+2，x+3，
由图形得，x+3=2x，解得x=3，
所以这个六边形的周长=2x+2（x+1）+2（x+2）+x+3
=7x+9
=7×3+9
=30．
所以六边形的周长为30．
设第二小的等边三角形的边长为x，而中间的小等边三角形的边长是1，
所以其它等边三角形的边长分别x+1，x+2，x+3，
由图形得，x+3=2x，解得x=3，
所以这个六边形的周长=2x+2（x+1）+2（x+2）+x+3
=7x+9
=7×3+9
=30．
所以六边形的周长为30．
点评：本题考查了等边三角形的性质：等边三角形的三边都相等，三个角都等于60°；找出等量关系，解一元一次方程是本题的关键；
练习册系列答案
名校课堂系列答案
相关题目
下列条件能得二线互相垂直的个数有（ ）
①一条直线与两条平行线中的一条直线垂直；
②邻补角的两条平分线；
③平行线的同旁内角的平分线；
④同时垂直于第三条直线的两条直线．
①一条直线与两条平行线中的一条直线垂直；
②邻补角的两条平分线；
③平行线的同旁内角的平分线；
④同时垂直于第三条直线的两条直线．
| A、4个 | B、3个 | C、2个 | D、1个 |
一个不等式组的解集在数轴上表示如图所示，则该不等式组的解集为（ ）| A、x＞-2 | B、x＜-2 |
| C、x＜1 | D、-2＜x＜1 |
已知：如图，∠BCP=∠A，∠AHB=∠APH，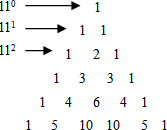
杨辉三角是数学之花，是中国古代数学的伟大成就．它有许多有趣的性质和用途，这个由数字排列成的三角形数就称为杨辉三角，如图，其中每一横行都表示（a+b）n（此处n=0，1，2，3，4，5，…）的展开式中各项的系数．