题目内容
如图，AB=4，BC=3，CD=13，AD=12，∠B=90°，求四边形ABCD的面积．
解：在Rt△ABC中，AC=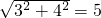
．
又因为52+122=132，
即AD2+AC2=CD2．
所以∠DAC=90°．
所以
=6+30=36．
分析：在Rt△ABC中可得直线AC的长，进而得出△ACD也为直角三角形，可求解其面积．
点评：熟练掌握勾股定理的运用，能够运用勾股定理求解一些简单的计算问题．
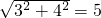．又因为52+122=132，
即AD2+AC2=CD2．
所以∠DAC=90°．
所以
=6+30=36．分析：在Rt△ABC中可得直线AC的长，进而得出△ACD也为直角三角形，可求解其面积．
点评：熟练掌握勾股定理的运用，能够运用勾股定理求解一些简单的计算问题．
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
如图，AB∥EF，BC∥DE，则图中与∠B相等的角有（ ）
如图，AB=AD，BC=CD，那么全等三角形的对数是（ ）
如图，AB∥ED，BC∥EF，AF=CD，且BC=6．
如图，AB∥CD，BC⊥AB，若AB=4cm，S△ABC=12cm2，求△ABD中AB边上的高等于
如图，AB=AD，BC=DC，要证∠B=∠D，则需要连接