题目内容
13. 如图,⊙O的直径AB=8,弦CD=4$\sqrt{3}$,且CD∥AB,判断CD为直径的圆与直线AB的位置关系,并说明理由.
如图,⊙O的直径AB=8,弦CD=4$\sqrt{3}$,且CD∥AB,判断CD为直径的圆与直线AB的位置关系,并说明理由.
分析 作OE⊥CD于E,连接OC,则CE=DE=$\frac{1}{2}$CD=2$\sqrt{3}$,∠OEC=90°,由勾股定理求出OE=2<2$\sqrt{3}$,即可得出CD为直径的圆与直线AB相交.
解答 解:CD为直径的圆与直线AB相交;理由如下:
作OE⊥CD于E,连接OC,如图所示: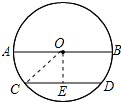
则CE=DE=$\frac{1}{2}$CD=2$\sqrt{3}$,∠OEC=90°,
∵⊙O的直径AB=8,
∴OC=OA=$\frac{1}{2}$AB=4,
由勾股定理得:OE=$\sqrt{O{C}^{2}-C{E}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2<2$\sqrt{3}$,
∴CD为直径的圆与直线AB相交.
点评 本题考查了直线与圆的位置关系、勾股定理;解决此类问题可通过比较圆心到直线距离d与圆半径大小关系即可判定.

练习册系列答案
相关题目




 如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的平移变换得到,图②中的图形还可以通过旋转变换得到.
如图,请画出一个图形经过两次轴对称变换之后得到的图形,其中图①中的两条对称轴是平行的,图②中的两条对称轴是垂直的.仔细观察上面的两个图形经过两次轴对称变换之后得到的图形.图①中的图形除经过两次轴对称变换得到之外,还可以通过我们学过的平移变换得到,图②中的图形还可以通过旋转变换得到.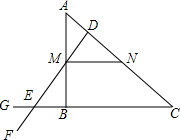 如图,在△ABC中,∠A=50°,点M在AB上,过点M作MN∥BC,交AC于点N,D是N上一点,连接DM并延长,交CB的延长线于点E.
如图,在△ABC中,∠A=50°,点M在AB上,过点M作MN∥BC,交AC于点N,D是N上一点,连接DM并延长,交CB的延长线于点E.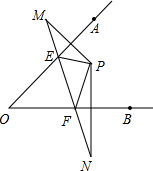 如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F. 如图,已知在等腰直角△ABC中,∠A=90度,CD平分∠ACB,DE⊥BC于E.若AC=10cm,则BD+DE=10cm.
如图,已知在等腰直角△ABC中,∠A=90度,CD平分∠ACB,DE⊥BC于E.若AC=10cm,则BD+DE=10cm.