题目内容
5.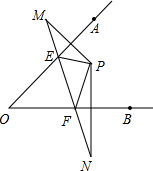 如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.
如图所示.点P在∠AOB的内部,点M、N分别是点P关于直线OA、OB的对称点,线段MN交OA、OB于点E、F.(1)若MN=20cm,求△PEF的周长.
(2)若∠AOB=35°,求∠EPF的度数.
分析 (1)根据轴对称的性质得出ME=PE,NF=PF,再由MN=20cm即可得出结论;
(2)要求∠EPF的度数,要在△EPF中进行,根据轴对称的性质和等腰三角形的性质找出与∠MPN的关系,利用已知∠AOB=35°可求出∠EPF,答案可得
解答 解:(1)∵点M、N分别是点P关于OA、OB的对称点,
∴ME=PE,NF=PF,MN=20cm,
∴ME+EF+NF=PE+EF+PF=MN=20cm,即△PEF的周长是20cm.
(2)如图,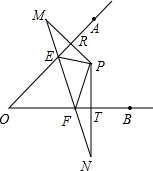
∵点M、N分别是点P关于直线0A、OB的对称点,
∴OA垂直平分PM,OB垂直平分PN,
∴∠PRE=∠PTF=90°,
∴在四边形OTPR中,
∴∠MPN+∠AOB=180°,
∵∠EPF+2∠M+2∠N=180°,
即∠MPN+∠M+∠N=180°,
∴∠M+∠N=∠AOB=35°
∴∠EPF=180°-35°×2=110°.
点评 本题主要考查了轴对称的性质、线段垂直平分线的性质,在计算的过程中运用了四边形的内角和和三角形的内角和定理及其推论.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
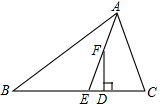 如图,在△ABC中,AE平分∠BAC,F为AE上一点,且FD⊥BC于点D,若∠C-∠B=40°,求∠EFD的度数.
如图,在△ABC中,AE平分∠BAC,F为AE上一点,且FD⊥BC于点D,若∠C-∠B=40°,求∠EFD的度数. 如图,⊙O的直径AB=8,弦CD=4$\sqrt{3}$,且CD∥AB,判断CD为直径的圆与直线AB的位置关系,并说明理由.
如图,⊙O的直径AB=8,弦CD=4$\sqrt{3}$,且CD∥AB,判断CD为直径的圆与直线AB的位置关系,并说明理由.