题目内容
13.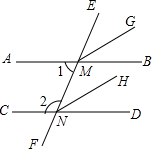 如图,直线EF分别交AB、CD于点M、N,MG平分∠EMB,NH平分∠END,并且MG∥NH,请说明∠1+∠2=180°的理由.
如图,直线EF分别交AB、CD于点M、N,MG平分∠EMB,NH平分∠END,并且MG∥NH,请说明∠1+∠2=180°的理由.
分析 根据平行线的性质得出∠EMG=∠ENH,根据角平分线定义求出∠EMB=2∠EMG,∠END=2∠ENH,推出∠EMB=∠END,根据平行线的判定得出AB∥CD,即可得出答案.
解答 解:理由是:∵MG∥NH,
∴∠EMG=∠ENH,
∵MG平分∠EMB,NH平分∠END,
∴∠EMB=2∠EMG,∠END=2∠ENH,
∴∠EMB=∠END,
∴AB∥CD,
∴∠1+∠2=180°.
点评 本题考查了平行线的性质和判定,角平分线定义的应用,能求出AB∥CD是解此题的关键,注意:①两直线平行,同位角相等,②同位角相等,两直线平行,③两直线平行,同旁内角互补.

练习册系列答案
相关题目
4.已知下列命题:
(1)若$\sqrt{(m-1)^{2}}$=m-1,则m≥1 (2)若a>b,则a2>ab
(3)平分弦的直径垂直于弦 (4)菱形的对角线互相平分
其中原命题与逆命题均为真命题的个数是( )
(1)若$\sqrt{(m-1)^{2}}$=m-1,则m≥1 (2)若a>b,则a2>ab
(3)平分弦的直径垂直于弦 (4)菱形的对角线互相平分
其中原命题与逆命题均为真命题的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.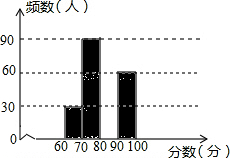 某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:
某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:
根据以上图表信息,解答下列问题:
(1)补全频数分布表和频数直方图;
(2)参赛的小明同学认为他的比赛成绩是所有参赛同学成绩的中位数,据此推断他的成绩落在80≤x<90分数段内;
(3)如果该校共有2000名学生参赛,比赛成绩80分以上(含80分)为“优秀”,请估计该校获得“优秀”等级的人数.
 某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:
某中学组织学生参加“社会主义核心价值观知识竞赛”,赛后随机抽查了部分参赛同学的成绩,整理并制成图表如下:| 分数段 | 频数 | 频率 |
| 60≤x<70 | 30 | 0.1 |
| 70≤x<80 | 90 | |
| 80≤x<90 | 0.4 | |
| 90≤x<100 | 60 | 0.2 |
(1)补全频数分布表和频数直方图;
(2)参赛的小明同学认为他的比赛成绩是所有参赛同学成绩的中位数,据此推断他的成绩落在80≤x<90分数段内;
(3)如果该校共有2000名学生参赛,比赛成绩80分以上(含80分)为“优秀”,请估计该校获得“优秀”等级的人数.
5.冬冬同学做了以下4道计算题:①(-1)2012=2012;②0-(-1)=1;③-$\frac{1}{2}$+$\frac{1}{3}$=-$\frac{1}{6}$;④$\frac{1}{2}$+(-$\frac{1}{2}$)=-1.请你帮他检查一下,他一共做对了( )
| A. | 4道题 | B. | 3道题 | C. | 2道题 | D. | 1道题 |
2.下列图形中,中心对称图形的个数是( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
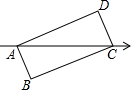 如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是-1,则对角线AC、BD的交点表示的数是( )
如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是-1,则对角线AC、BD的交点表示的数是( )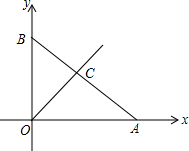 如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+3$的图象分别交x轴,y轴交于A,B两点,与一次函数y=x的图象交于第一象限内的点C.
如图,在平面直角坐标系中,一次函数y=-$\frac{1}{2}x+3$的图象分别交x轴,y轴交于A,B两点,与一次函数y=x的图象交于第一象限内的点C.