题目内容
18.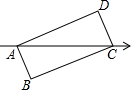 如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是-1,则对角线AC、BD的交点表示的数是( )
如图,矩形ABCD的对角线AC与数轴重合(点C在正半轴上),AB=5,BC=12,点A表示的数是-1,则对角线AC、BD的交点表示的数是( )| A. | 5.5 | B. | 5 | C. | 6 | D. | 6.5 |
分析 连接BD交AC于E,由矩形的性质得出∠B=90°,AE=$\frac{1}{2}$AC,由勾股定理求出AC,得出OE,即可得出结果.
解答 解:连接BD交AC于E,如图所示: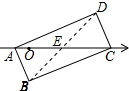
∵四边形ABCD是矩形,
∴∠B=90°,AE=$\frac{1}{2}$AC,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{5}^{2}+1{2}^{2}}$=13,
∴AE=6.5,
∵点A表示的数是-1,
∴OA=1,
∴OE=AE-OA=5.5,
∴点E表示的数是5.5,
即对角线AC、BD的交点表示的数是5.5;
故选:A.
点评 本题考查了矩形的性质、勾股定理、实数与数轴;熟练掌握矩形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
相关题目
9. 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )
 将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为点B′,折痕为EF,已知AB=AC=3,BC=4,若以点B′,F,C为顶点的三角形与△ABC相似,那么BF的长度是( )| A. | $\frac{12}{7}$ | B. | 2 | C. | $\frac{12}{5}$或2 | D. | $\frac{12}{7}$或2 |
6.下列根式与$\sqrt{3}$是同类二次根式的是( )
| A. | $\sqrt{32}$ | B. | $\sqrt{12}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{\frac{2}{25}}$ |
3.将一个正方形按下列要求分割成4块:
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形,请你按照上述两个要求,分别在图1,图2,图3的正方形中画出3种不同的分割方法(不写画法)
(1)分割后的整个图形必须是轴对称图形;
(2)所分得的4块图形是全等图形,请你按照上述两个要求,分别在图1,图2,图3的正方形中画出3种不同的分割方法(不写画法)

10.为了描述我市梵净山风景区“金顶”处某一天气温变化情况,应该选择绘制的统计图类型是( )
| A. | 折线统计图 | B. | 条形统计图 | C. | 扇形统计图 | D. | 复式统计图 |
8.若点A(2,m)在抛物线y=x2上,则m的值为( )
| A. | 2 | B. | ±2 | C. | 4 | D. | ±4 |
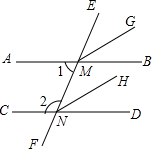 如图,直线EF分别交AB、CD于点M、N,MG平分∠EMB,NH平分∠END,并且MG∥NH,请说明∠1+∠2=180°的理由.
如图,直线EF分别交AB、CD于点M、N,MG平分∠EMB,NH平分∠END,并且MG∥NH,请说明∠1+∠2=180°的理由. 如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F.若BF=DE,则图中的全等三角形最多有6对.
如图,O为平行四边形ABCD对角线AC、BD的交点,EF经过点O,且与边AD、BC分别交于点E、F.若BF=DE,则图中的全等三角形最多有6对.