题目内容
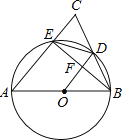
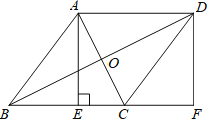
【题目】如图,在![]() 中,点
中,点![]() 在
在![]() 上,连接
上,连接![]() ,点
,点![]() 在
在![]() 上,
上,![]() 的延长线交射线
的延长线交射线![]() 于点
于点![]() .
.

(1)若点![]() 是
是![]() 边上的中点,且
边上的中点,且![]() ,求
,求![]() 的值.
的值.
(2)若点![]() 是
是![]() 边上的中点,且
边上的中点,且![]() ,求
,求![]() 的值.(用含
的值.(用含![]() 的代数式表示),试写出解答过程.
的代数式表示),试写出解答过程.
(3)探究三:若![]() ,且
,且![]() ,请直接写出
,请直接写出![]() 的值(不写解答过程).
的值(不写解答过程).
【答案】(1)2;(2)![]() ;(3)
;(3)![]()
【解析】
(1)过点E作EH∥AB交BG于H,证明△ABF∽△EHF,则![]() ,所以AB=4EH;同理证明△BHE∽△BGC,得CG=2EH,所以
,所以AB=4EH;同理证明△BHE∽△BGC,得CG=2EH,所以![]() ;
;
(2)由(1)得![]() ,
,![]() ,将(1)中的4换成m,代入计算即可得出结论:
,将(1)中的4换成m,代入计算即可得出结论:![]() ;
;
(3)先由△ABF∽△EHF,则![]() ,所以AB=mEH;再由△BHE∽△BGC,得
,所以AB=mEH;再由△BHE∽△BGC,得![]() ,
,![]() .
.
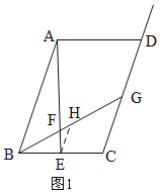
解:(1)如图![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ 四边形![]() 是平行四边形,
是平行四边形,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
又∵ ![]() 是
是![]() 的中点,
的中点,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ;
;
(2)由(1)得![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ;
;
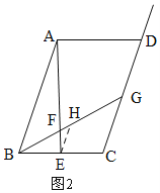
(3)如图![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于
于![]() ,
,
则![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ 四边形![]() 是平行四边形,
是平行四边形,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∵ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴ 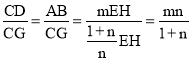 .
.
(1)过点![]() 作
作![]() 交
交![]() 于
于![]() ,先证明
,先证明![]() ,则
,则![]() ,所以
,所以![]() ;同理证明
;同理证明![]() ,得
,得![]() ,所以
,所以![]() ;
;
(2)由(1)得![]() ,
,![]() ,将(1)中的
,将(1)中的![]() 换成
换成![]() ,代入计算即可得出结论:
,代入计算即可得出结论:![]() ;
;
(3)先由![]() ,则
,则![]() ,所以
,所以![]() ;再由
;再由![]() ,得
,得![]() ,代入可得结论:
,代入可得结论: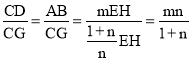 .
.

练习册系列答案
相关题目