题目内容
1.抛物线y=ax2+bx+c的顶点为(3,-2),且在x轴上截出的线段长为8,求这个二次函数的解析式.分析 利用顶点坐标公式得出两个方程,再利用抛物线在x轴上截得的线段长公式得到第三个方程,联立方程组求得a、b、c得出答案即可.
解答 解:∵抛物线y=ax2+bx+c的顶点为(3,-2),
∴-$\frac{b}{2a}$=3,$\frac{4ac-{b}^{2}}{4a}$=-2,
∵x轴上截出的线段长为8,
∴$\frac{\sqrt{{b}^{2}-4ac}}{|a|}$=8,
由题意得$\left\{\begin{array}{l}{-\frac{b}{2a}=3}\\{\frac{4ac-{b}^{2}}{4a}=-2}\\{\frac{\sqrt{{b}^{2}-4ac}}{|a|}=8}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{1}{8}}\\{b=-\frac{3}{4}}\\{c=-\frac{7}{8}}\end{array}\right.$,
∴抛物线y=$\frac{1}{8}$x2-$\frac{3}{4}$x-$\frac{7}{8}$.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.

练习册系列答案
相关题目
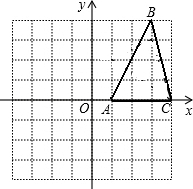 如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系.
如图所示,每一个小方格都是边长为1的单位正方形.△ABC的三个顶点都在格点上,以点O为坐标原点建立平面直角坐标系. 如图所示的直线ABC为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(min)之间的函数关系的图象.由图象可知,通话2min需付电话费1.4元,通话5min需付电话费4.4元.
如图所示的直线ABC为甲地向乙地打长途电话所需付的电话费y(元)与通话时间t(min)之间的函数关系的图象.由图象可知,通话2min需付电话费1.4元,通话5min需付电话费4.4元. 如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.
如图,AB和CD表示两根直立于地面的柱子,AD和BC表示起固定作用的两根钢筋,AD与BC的交点为M,已知AB=10m,CD=15m,求点M离地面的高度MH.