题目内容
4.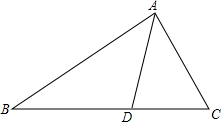 △ABC中,D是BC上的点,AD平分∠BAC,BD=2DC,若∠BAC=60°,求∠B.
△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC,若∠BAC=60°,求∠B.
分析 根据角平分线的轴对称性,在AB上堆取AE=AC,即可得到△AED≌△ACD,从而DE=DC,∠ADE=∠ADC,再作EF∥AD交BD于F,由平行线的性质可推出F为BD中点,从而E为AB中点.由于∠BAC=60°,则三角形AEC是等边三角形,于是BE=EC,然后∠B的度数一目了然.
解答 解:在AB上堆取AE=AC,连接DE、EC,如图,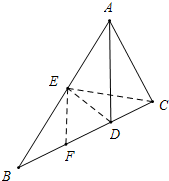
易得△AED≌△ACD,
∴DE=DC,∠ADE=∠ADC,
作EF∥AD交BC于F,
∴∠EFD=∠ADC,∠FED=∠ADE,
∴∠DFE=∠DEF,
即DF=DE=DC,
∵BD=2DC,
∴BF=FD,
∵EF∥AD,BF=FD,
∴BE=AE,
∵∠BAC=60°
∴△AEC是等边三角形,
∴BE=EC,
∴∠B=∠ECB,
∵∠B+∠ECB=∠AEC=60°,
∴2∠B=60°,
∴∠B=30°.
点评 本题主要考查了角平分线的性质、全等三角形的判定与性质、平行线的性质、等边三角形的判定与性质、三角形外角性质等知识点,题虽小,难度却较大.根据角平分线在角两边截取线段相等,进而构造全等三角形,是常用辅助线,要熟练掌握.

练习册系列答案
相关题目
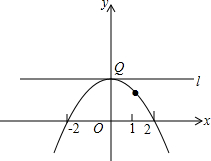 在平面直角坐标系xOy中,已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A(2,0)和点B(1,$\frac{3}{4}$),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.
在平面直角坐标系xOy中,已知二次函数y=-$\frac{1}{4}{x}^{2}+mx+n$的图象经过点A(2,0)和点B(1,$\frac{3}{4}$),直线l经过抛物线的顶点且与y轴垂直,垂足为Q.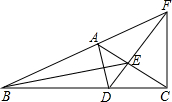 如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.
如图,△ABC中,∠BAC=120°,AD为△ABC的内角平分线,CF为△ABC的外角平分线,交BA的延长线于点F,连接DF交AC于E,连接BE,求证:BE平分∠ABC.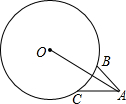 如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.
如图,△ABC中,BC=4,∠BAC=45°,以$4\sqrt{2}$为半径,过B、C两点作⊙O,连OA,则线段OA的最大值为2$\sqrt{2}$+2+2$\sqrt{7}$.



 ”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
”来表示我们所使用的自然数,如自然数1~19的表示见下表,另外在任何数的下方加一个卵形,就表示把这个数扩大到它的20倍,如表中20和100的表示.
 表示的自然数是18;
表示的自然数是18; .
.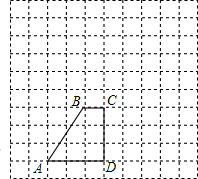 (1)如图在10×10的方格纸中,梯形ABCD是直角梯形,请在图中以CD为对称轴画一个关于直线CD对称的直角梯形EFCD,使它与梯形ABCD构成一个等腰梯形AEFB.(不要求写作法)
(1)如图在10×10的方格纸中,梯形ABCD是直角梯形,请在图中以CD为对称轴画一个关于直线CD对称的直角梯形EFCD,使它与梯形ABCD构成一个等腰梯形AEFB.(不要求写作法)