题目内容
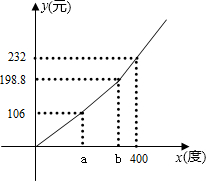 自2012年6月1日起,全国实施了阶梯电价.某省出台了阶梯电价方案:电价分“三档”收费,第一档为a度,居民用电量低于a度的部分,执行现行的标准电价(0.53元/度);第二档为a~b度,居民月用电量在a~b之间的部分,电价在一档电价的基础上提高0.05元/度;第三档为超过b度,居民月用电量高于b度的部分,电价在一档电价的基础上提高m元/度.实施阶梯电价后,月电费y(元)与月用电量x(度)之间的函数关系如图所示.
自2012年6月1日起,全国实施了阶梯电价.某省出台了阶梯电价方案:电价分“三档”收费,第一档为a度,居民用电量低于a度的部分,执行现行的标准电价(0.53元/度);第二档为a~b度,居民月用电量在a~b之间的部分,电价在一档电价的基础上提高0.05元/度;第三档为超过b度,居民月用电量高于b度的部分,电价在一档电价的基础上提高m元/度.实施阶梯电价后,月电费y(元)与月用电量x(度)之间的函数关系如图所示.(1)求a,b,m的值;
(2)求y与x之间函数关系式,并写出自变量x的取值范围.
考点:一次函数的应用
专题:
分析:(1)a度共106元,每度是0.53元,据此即可求得a的值;
根据第一阶段是106元,(b-a)度,每度是0.58元,则b度共198.8元,据此即可求得第段的度数,求得b的值;
根据400度付款232元,即可求得第三档的价格,从而求得m的值;
(2)根据(1)中的三个档的价格,以及收费标准即可求解.
根据第一阶段是106元,(b-a)度,每度是0.58元,则b度共198.8元,据此即可求得第段的度数,求得b的值;
根据400度付款232元,即可求得第三档的价格,从而求得m的值;
(2)根据(1)中的三个档的价格,以及收费标准即可求解.
解答:解:(1)a=106÷0.53=200(度),
(198.8-106)÷(0.53+0.05)=160,
则b=200+160=360(度),
(232-198.8)÷(400-360)=0.83(元),
则m=0.83-0.53=0.3(元);
(2)当x≤200时,y与x的函数关系式是y=0.53x;
当200<x≤360时,y与x的函数关系式是:y=106+0.58(x-200),即y=0.58x;
当x≥360时,y=198.8+0.83(x-360),即y=0.83x-100.
(198.8-106)÷(0.53+0.05)=160,
则b=200+160=360(度),
(232-198.8)÷(400-360)=0.83(元),
则m=0.83-0.53=0.3(元);
(2)当x≤200时,y与x的函数关系式是y=0.53x;
当200<x≤360时,y与x的函数关系式是:y=106+0.58(x-200),即y=0.58x;
当x≥360时,y=198.8+0.83(x-360),即y=0.83x-100.
点评:本题考查的是用一次函数解决实际问题,解答一次函数的应用问题中,要注意自变量的取值范围还必须使实际问题有意义.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
抛物线y=x2向下平移一个单位得到抛物线( )
| A、y=(x+1)2 |
| B、y=(x-1)2 |
| C、y=x2+1 |
| D、y=x2-1 |
 用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图.
用小立方体搭一个几何体,使它从正面、从上面看到的形状图如图所示,这样的几何体只有一种吗?它最多需要多少个小立方体?它最少需要多少个小立方体?请你画出这两种情况下的从左面看到的形状图. 如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.
如图,∠ABC=∠ADC=90°,M、N分别是AC、BD的中点.求证:MN⊥BD.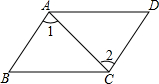 如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?
如图,AB∥CD,AB=CD.问:△ABC和△CDA是全等三角形吗?为什么?