题目内容
10.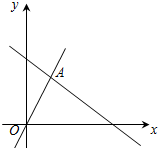 如图,函数y=2x和y=-$\frac{2}{3}$x+4的图象相交于点A,
如图,函数y=2x和y=-$\frac{2}{3}$x+4的图象相交于点A,(1)求点A的坐标;
(2)根据图象,直接写出不等式2x≥-$\frac{2}{3}$x+4的解集.
分析 (1)联立两直线解析式,解方程组即可得到点A的坐标;
(2)根据图形,找出点A右边的部分的x的取值范围即可.
解答 解:(1)由$\left\{\begin{array}{l}{y=2x}\\{y=-\frac{2}{3}x+4}\end{array}\right.$,解得:$\left\{\begin{array}{l}{x=\frac{3}{2}}\\{y=3}\end{array}\right.$,
∴A的坐标为($\frac{3}{2}$,3);
(2)由图象,得不等式2x≥-$\frac{2}{3}$x+4的解集为:x≥$\frac{3}{2}$.
点评 本题考查了一次函数与一元一次不等式,联立两直线解析式求交点坐标的方法,求一次函数与一元一次不等式关键在于准确识图,确定出两函数图象的对应的函数值的大小.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
1. 如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )
如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )
 如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )
如图,AB是⊙O的直径,∠BAC=30°,CD⊥AB于点E,BE=2,则⊙O的半径为( )| A. | 8 | B. | 6 | C. | 4 | D. | 2 |
15.下列几何体中左视图是矩形的共有( )


| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
2.若代数式$\frac{x-2}{x+2}$的值为0,则x等于( )
| A. | 2 | B. | -2 | C. | 0 | D. | 2,-2 |
 如图,在⊙O中,AB是直径,CD是弦,∠D=40°,则∠AOC=100度.
如图,在⊙O中,AB是直径,CD是弦,∠D=40°,则∠AOC=100度. 如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.
如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.