题目内容
19. 如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.
如图,已知△ABC≌△A′B′C′,AD,A′D′分别是∠BAC和∠B′A′C′的角平分线,试说明AD=A′D′的理由.
分析 首先由△ABC≌△A′B′C′,根据全等三角形的性质得出AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,再由角平分线的定义可得∠BAD=∠B′A′D′,再利用ASA定理证明△ABD≌△A′B′D′可得AD=A′D′.
解答 证明:∵△ABC≌△A′B′C′,
∴AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′,
∵AD和A′D′分别是△ABC和△A′B′C′的角平分线,
∴∠BAD=$\frac{1}{2}$∠BAC,∠B′A′D′=$\frac{1}{2}$∠B′A′C′,
∴∠BAD=∠B′A′D′.
在△ABD和△A′B′D′中,
$\left\{\begin{array}{l}{∠BAD=∠B′A′D′}\\{AB=A′B′}\\{∠B=∠B′}\end{array}\right.$,
∴△ABD≌△A′B′D′(ASA),
∴AD=A′D′.
点评 此题主要考查了全等三角形的判定与性质,关键是掌握全等三角形的判定方法:SSS、SAS、ASA、AAS、HL.根据全等三角形的对应边相等、对应角相等得出AB=A′B′,∠B=∠B′,∠BAC=∠B′A′C′是解题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
11.关于的分式方程$\frac{-2-a}{x-1}$=1的解是正数,则a的取值范围是( )
| A. | a>-1 | B. | a>-1且a≠0 | C. | a<-1 | D. | a<-1且a≠-2 |
8.下列各数中,最小的数是( )
| A. | -3 | B. | |-4| | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
 如图是小明设计的用激光笔测量城墙高度的示意图,在点P处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,AB=1.2米,BP=1.8米,PD=12米,那么该城墙高度CD=8米.
如图是小明设计的用激光笔测量城墙高度的示意图,在点P处水平放置一面平面镜,光线从点A出发经平面镜反射后刚好射到城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,AB=1.2米,BP=1.8米,PD=12米,那么该城墙高度CD=8米.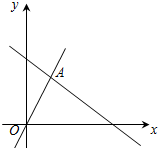 如图,函数y=2x和y=-$\frac{2}{3}$x+4的图象相交于点A,
如图,函数y=2x和y=-$\frac{2}{3}$x+4的图象相交于点A, 如图,平行四边形ABCD中,AD=2,E在AD边上,BE=2.8,CF⊥CE交BE于F,若∠CED=3∠BEC,则线段BF的长为1.2.
如图,平行四边形ABCD中,AD=2,E在AD边上,BE=2.8,CF⊥CE交BE于F,若∠CED=3∠BEC,则线段BF的长为1.2.