题目内容
2. 如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AO∥BC,点A的坐标为(0,6),∠AOB=60°,OA=AB.
如图,在平面直角坐标系中,点O是坐标原点,四边形AOCB是梯形,AO∥BC,点A的坐标为(0,6),∠AOB=60°,OA=AB.(1)求点B的坐标;
(2)点P从O点出发,沿线段OB以1个单位/秒的速度向终点B匀速运动,点Q从B点出发,沿线段BA以1个单位/秒的速度向终点A匀速运动,设△CPQ的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(直接写出自变量t的取值范围);
(3)在(2)的条件下,当$\frac{CP}{PQ}=\frac{1}{{\sqrt{3}}}$时,求tan∠PQC的值.
分析 (1)证得△AOB是等边三角形,即可证得BC=$\frac{1}{2}$OB=3,OC=$\frac{\sqrt{3}}{2}$OB=3$\sqrt{3}$,从而证得B点的坐标为(3$\sqrt{3}$,3);
(2)作PM⊥BC于M.PN⊥AB于N,QK⊥BC,交CB的延长线于K,由OP=BQ=t,PB=6-t,根据解直角三角形得出PM=PN=$\frac{\sqrt{3}}{2}$(6-t),QK=$\frac{\sqrt{3}}{2}$t,如图2,根据S△CPQ=S△PQB+S△PCB-S△BCQ,如图3,根据S△CPQ=S△BCQ-S△PQB-S△PCB求得即可;
(3)根据勾股定理分别求得PQ、PC、QC的长度,过P作PH⊥QC,设CH=x,则QH=7-x,过P作PH⊥QC,设CH=x,则QH=7-x,根据勾股定理求得列出关于x的方程,解方程求得x的值,从而求得QH、PH的值,即可求得tan∠PQC的值.
解答  解:(1)∵点A的坐标为(0,6),
解:(1)∵点A的坐标为(0,6),
∴OA=6,
∵∠AOB=60°,OA=AB,
∴∠AOB=∠ABO=60°,
∴△AOB是等边三角形,
∴OB=OA=6,
∵∠AOC=90°,
∵AO∥BC,
∴∠BCO=90°,
∴∠BOC=30°,
∴BC=$\frac{1}{2}$OB=3,OC=$\frac{\sqrt{3}}{2}$OB=3$\sqrt{3}$,
∴B(3$\sqrt{3}$,3);
(2)作PM⊥BC于M.PN⊥AB于N,QK⊥BC,交CB的延长线于K,
∴∠BOC=30°,∠BCO=90°,
∴∠OBC=60°,
∴∠OBC=∠ABO=60°,
∴PM=PN,∠ABK=60°,
∵OP=BQ=t,
∴PB=6-t,
∴PM=PN=$\frac{\sqrt{3}}{2}$(6-t),QK=$\frac{\sqrt{3}}{2}$t,
①如图2,S△CPQ=S△PQB+S△PCB-S△BCQ=$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$(6-t)+$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$(6-t)-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$t=-$\frac{\sqrt{3}}{4}$t2+$\frac{9\sqrt{3}}{2}$,
即S△CPQ=-$\frac{\sqrt{3}}{4}$t2+$\frac{9\sqrt{3}}{2}$(0≤t$<3\sqrt{2}$);
②如图3, S△CPQ=S△BCQ-S△PQB-S△PCB=$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$t-$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$(6-t)-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$(6-t)=$\frac{\sqrt{3}}{4}$t2-$\frac{9\sqrt{3}}{2}$,
S△CPQ=S△BCQ-S△PQB-S△PCB=$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$t-$\frac{1}{2}$×t×$\frac{\sqrt{3}}{2}$(6-t)-$\frac{1}{2}$×3×$\frac{\sqrt{3}}{2}$(6-t)=$\frac{\sqrt{3}}{4}$t2-$\frac{9\sqrt{3}}{2}$,
即S△CPQ=$\frac{\sqrt{3}}{4}$t2-$\frac{9\sqrt{3}}{2}$(3$\sqrt{2}$<x<6);
综上,S与t之间的函数关系式为:S=$\left\{\begin{array}{l}{-\frac{\sqrt{3}}{4}{t}^{2}+\frac{9\sqrt{3}}{2}(0≤t<3\sqrt{2})}\\{\frac{\sqrt{3}}{4}{t}^{2}-\frac{9\sqrt{3}}{2}(3\sqrt{2}<t<6)}\end{array}\right.$;
(3)如图2,在△BPQ中,BQ=t,BP=6-t,∠PBQ=60°,
∴PN=$\frac{\sqrt{3}}{2}$(6-t),BN=$\frac{1}{2}$(6-t),
∴QN=t-$\frac{1}{2}$(6-t)=$\frac{3}{2}$t-3,
∴PQ=$\sqrt{Q{N}^{2}+P{N}^{2}}$=$\sqrt{(\frac{3}{2}t-3)^{2}+[\frac{\sqrt{3}}{2}(6-t)]^{2}}$=$\sqrt{3{t}^{2}-18t+36}$,
在△BPC中,BC=3,BP=6-t,∠PBC=60°,
∴PM=$\frac{\sqrt{3}}{2}$(6-t),BM=$\frac{1}{2}$(6-t),
∴MC=3-$\frac{1}{2}$(6-t)=$\frac{1}{2}$t,
∴PC=$\sqrt{P{M}^{2}+M{C}^{2}}$=$\sqrt{[\frac{\sqrt{3}}{2}(6-t)]^{2}+(\frac{1}{2}t)^{2}}$=$\sqrt{{t}^{2}-9t+27}$,
∵$\frac{CP}{PQ}=\frac{1}{{\sqrt{3}}}$,
∴$\frac{\sqrt{{t}^{2}-9t+27}}{\sqrt{3{t}^{2}-18t+36}}$=$\frac{1}{\sqrt{3}}$,
整理得9t=45,
∴t=5,
∴PQ=$\sqrt{21}$,PC=$\sqrt{7}$,BQ=5,
∴BK=$\frac{5}{2}$,QK=$\frac{5\sqrt{3}}{2}$,
∴QC=$\sqrt{C{K}^{2}+Q{K}^{2}}$=$\sqrt{(3+2.5)^{2}+(\frac{5\sqrt{3}}{2})^{2}}$=7,
过P作PH⊥QC,设CH=x,则QH=7-x,
根据勾股定理,PC2-CH2=PQ2-QH2,
∴7-x2=21-(7-x)2,
解得x=$\frac{35}{14}$=$\frac{5}{2}$,
∴CH=$\frac{5}{2}$,
∴PH=$\sqrt{P{C}^{2}-C{H}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴tan∠PQC=$\frac{PH}{QH}$=$\frac{\frac{\sqrt{3}}{2}}{7-\frac{5}{2}}$=$\frac{\sqrt{3}}{9}$.
点评 本题是四边形的综合题,考查了等边三角形的判定和性质,梯形的性质,解直角三角形,勾股定理的应用以及三角形面积等,分类讨论思想的运用是解题的关键.

 名校课堂系列答案
名校课堂系列答案| A. | 5 | B. | 94 | C. | 45 | D. | -4 |
| A. | 相等的圆心角所对的弦相等 | |
| B. | 过圆心且平分弦的直线一定垂直于该弦 | |
| C. | 经过半径的端点且垂直于该半径的直线是圆的切线 | |
| D. | 相交两圆的连心线一定垂直且平分公共弦 |

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | $y=\frac{x^2}{3}$ | B. | y=2x2+$\frac{1}{x}$ | C. | $y=\frac{1}{x^2}$ | D. | y=2x+3 |
 如图,在△ABC中,点D,E分别在边A B,AC上,DE∥BC,已知EC=6,$\frac{AD}{DB}$=$\frac{2}{3}$,则AE的长是( )
如图,在△ABC中,点D,E分别在边A B,AC上,DE∥BC,已知EC=6,$\frac{AD}{DB}$=$\frac{2}{3}$,则AE的长是( ) 有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应挖在何处?请在图中标出井的位置,并说明理由.
有A,B,C三农户准备一起挖一口井,使它到三农户家的距离相等,这口井应挖在何处?请在图中标出井的位置,并说明理由.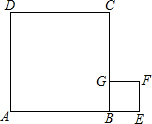 如图,点A、B、E在一直线上,且四边形ABCD和四边形BEFG都是正方形,在图中画一个正方形,使所画的正方形的面积为正方形ABCD与正方形BEFG的面积和(直接画出图形即可).
如图,点A、B、E在一直线上,且四边形ABCD和四边形BEFG都是正方形,在图中画一个正方形,使所画的正方形的面积为正方形ABCD与正方形BEFG的面积和(直接画出图形即可).