题目内容
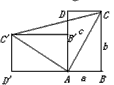
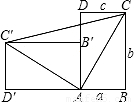
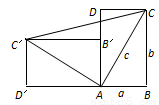
一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的验证方法.如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB=a,BC=b,AC=c，请利用四边形BCC′D′的面积验证勾股定理：a2+b2=c2.
【答案】
见解析
【解析】本题考查了勾股定理的证明
对直角梯形BCC′D′根据等面积法即可证得结果。
∵ 四边形BCC′D′为直角梯形，
∴S梯形BCC′D′=
(BC+C′D′)·BD′=
.
∵Rt△ABC≌Rt△AB′C′，
∴∠BAC=∠BAC′.
∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°.
∴S梯形BCC′D′=S△ABC+S△CAC′+S△D′AC′=
ab+c2+ab=
.
∴=.
∴a2+b2=c2.
练习册系列答案
相关题目
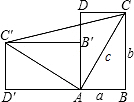一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的验证方法．如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB=a，BC=b，AC=c，请利用四边形BCC′D′的面积验证勾股定理：a2+b2=c2．
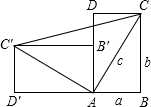侧面ABCD（是一个长方形）倒下到AB′C′D′的位置，连接CC′，设AB=a，BC=b，AC=c．
