题目内容
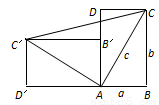
 一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
一个直立的火柴盒在桌面上倒下,启迪人们发现了勾股定理的一种新的验证方法.如图,火柴盒的一个侧面ABCD倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c,请利用四边形BCC′D′的面积验证勾股定理:a2+b2=c2.
分析:四边形BCC′D′的面积从大的一方面来说属于直角梯形,可利用直角梯形的面积公式进行表示从组成来看,由三个直角三角形组成.应利用三角形的面积公式来进行表示.
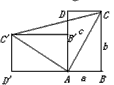
解答: 证明:四边形BCC′D′为直角梯形,
证明:四边形BCC′D′为直角梯形,
∴S梯形BCC′D′=
(BC+C′D′)•BD′=
,
又∵∠AB′C′=90°,Rt△ABC≌Rt△AB′C′
∴∠BAC=∠B′AC′.
∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°;
∴S梯形BCC′D′=S△ABC+S△CAC′+S△D′AC′=
ab+
c2+
ab=
;
∴
=
;
∴a2+b2=c2.
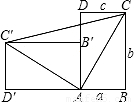
 证明:四边形BCC′D′为直角梯形,
证明:四边形BCC′D′为直角梯形,∴S梯形BCC′D′=
| 1 |
| 2 |
| (a+b)2 |
| 2 |
又∵∠AB′C′=90°,Rt△ABC≌Rt△AB′C′
∴∠BAC=∠B′AC′.
∴∠CAC′=∠CAB′+∠B′AC′=∠CAB′+∠BAC=90°;
∴S梯形BCC′D′=S△ABC+S△CAC′+S△D′AC′=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| c2+2ab |
| 2 |
∴
| (a+b)2 |
| 2 |
| c2+2ab |
| 2 |
∴a2+b2=c2.
点评:证明勾股定理时,需注意:组成的图形的面积有两种表示方法:大的面积的表示方法和各个组成部分的面积的和.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
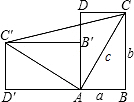
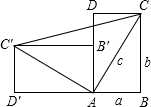 侧面ABCD(是一个长方形)倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c.
侧面ABCD(是一个长方形)倒下到AB′C′D′的位置,连接CC′,设AB=a,BC=b,AC=c.