题目内容
反比例函数y=
与一次函数y=kx+1交于点P(
,m).
(1)求反比例函数和一次函数的解析式;
(2)若反比例函数与直线的另一个交点是Q,反比例函数上的一点M满足:∠PQM=60°,求M的坐标.
| k |
| x |
| 1 |
| 2 |
(1)求反比例函数和一次函数的解析式;
(2)若反比例函数与直线的另一个交点是Q,反比例函数上的一点M满足:∠PQM=60°,求M的坐标.
考点:反比例函数综合题,待定系数法求一次函数解析式,待定系数法求反比例函数解析式,反比例函数与一次函数的交点问题,勾股定理,解直角三角形的应用
专题:计算题,综合题
分析:(1)由于点P在两个函数的图象上,因此点P的坐标满足两个函数解析式,只需把点P的坐标代入两个函数解析式,解出k和m,就可求出两个函数解析式.
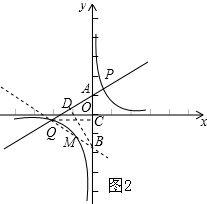
(2)由于点P、点Q确定,∠PQM=60°,因此直线QM确定,要求点M的坐标,只需先求出直线QM的解析式,然后通过解方程(组)就可求出点M的坐标.如图2,在△ABQ中,∠AQB已知,AQ及tan∠QAB都可求,可以通过构建直角三角形,利用锐角三角函数和勾股定理求出AB长,进而求出该直线QM与y轴的交点B的坐标,然后求出直线QM的解析式,就可求出点M的坐标.
(2)由于点P、点Q确定,∠PQM=60°,因此直线QM确定,要求点M的坐标,只需先求出直线QM的解析式,然后通过解方程(组)就可求出点M的坐标.如图2,在△ABQ中,∠AQB已知,AQ及tan∠QAB都可求,可以通过构建直角三角形,利用锐角三角函数和勾股定理求出AB长,进而求出该直线QM与y轴的交点B的坐标,然后求出直线QM的解析式,就可求出点M的坐标.
解答: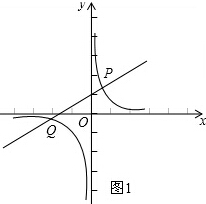 解:(1)如图1,
解:(1)如图1,
∵点P(
,m)在反比例函数y=
与一次函数y=kx+1的图象上,
∴
,
解得:
.
则反比例函数的解析式为y=
,一次函数的解析式为y=
x+1.
(2)设直线PQ与y轴交于点A,直线QM与y轴交于点B.
过点Q作QC⊥y轴,垂足为C;
过点B作BD⊥AQ,垂足为D,如图2所示.
联立两函数解析式得:
,
解得:
或
.
∴P(
,
)、Q(-2,-
).
∵点A是直线y=
x+1与y轴的交点,
∴点A坐标为(0,1).
在Rt△QCA中,
∵QC=2,AC=1-(-
)=
,
∴QA=
,tan∠QAC=
=
.
∵tan∠QAC=
=
>1,
∴∠QAC>45°.
∴∠AQC<45°.
∵∠PQM=60°,
∴M只可能在第三象限.
在Rt△ADB中,
tan∠DAB=
=
.
在Rt△QDB中,
tan∠DQB=
=tan60°=
.
设DA=2x,
则DB=3x,DQ=
x.
∵QA=QD+DA
═
x+2x
=
,
∴x=
.
∵BD⊥AD,DA=2x,DB=3x
∴AB=
x=
.
∴OB=AB-OA=
.
∴点B的坐标为(0,-
).
设直线QM的解析式为y=ax-
,
∵Q(-2,-
)在直线QM上,
∴-2a-
=-
,
∴a=
.
∴直线QM的解析式为y=
x-
.
设点M的坐标为(x,y),
∵点M是反比例函数y=
图象与直线QB的一个交点,
∴y=
x-
=
.
整理得:(13
-24)x2-(49-26
)x-2=0.
则(x+2)[(13
-24)x-1]=0.
解得:x1=-2,x2=-
.
∵点M与点Q不重合,
∴x≠-2.
∴x=-
.
∴y=
=
.
∴点M的坐标为(-
,
).
 解:(1)如图1,
解:(1)如图1,∵点P(
| 1 |
| 2 |
| k |
| x |
∴
|
解得:
|
则反比例函数的解析式为y=
| 2 |
| 3x |
| 2 |
| 3 |
(2)设直线PQ与y轴交于点A,直线QM与y轴交于点B.
过点Q作QC⊥y轴,垂足为C;
过点B作BD⊥AQ,垂足为D,如图2所示.
联立两函数解析式得:
|
解得:
|
|

∴P(
| 1 |
| 2 |
| 4 |
| 3 |
| 1 |
| 3 |
∵点A是直线y=
| 2 |
| 3 |
∴点A坐标为(0,1).
在Rt△QCA中,
∵QC=2,AC=1-(-
| 1 |
| 3 |
| 4 |
| 3 |
∴QA=
2
| ||
| 3 |
| QC |
| AC |
| 3 |
| 2 |
∵tan∠QAC=
| QC |
| AC |
| 3 |
| 2 |
∴∠QAC>45°.
∴∠AQC<45°.
∵∠PQM=60°,
∴M只可能在第三象限.
在Rt△ADB中,
tan∠DAB=
| DB |
| DA |
| 3 |
| 2 |
在Rt△QDB中,
tan∠DQB=
| DB |
| DQ |
| 3 |
设DA=2x,
则DB=3x,DQ=
| 3 |
∵QA=QD+DA
═
| 3 |
=
2
| ||
| 3 |
∴x=
2
| ||
3(
|
∵BD⊥AD,DA=2x,DB=3x
∴AB=
| 13 |
52-26
| ||
| 3 |
∴OB=AB-OA=
49-26
| ||
| 3 |
∴点B的坐标为(0,-
49-26
| ||
| 3 |
设直线QM的解析式为y=ax-
49-26
| ||
| 3 |
∵Q(-2,-
| 1 |
| 3 |
∴-2a-
49-26
| ||
| 3 |
| 1 |
| 3 |
∴a=
13
| ||
| 3 |
∴直线QM的解析式为y=
13
| ||
| 3 |
49-26
| ||
| 3 |
设点M的坐标为(x,y),
∵点M是反比例函数y=
| 2 |
| 3x |
∴y=
13
| ||
| 3 |
49-26
| ||
| 3 |
| 2 |
| 3x |
整理得:(13
| 3 |
| 3 |
则(x+2)[(13
| 3 |
解得:x1=-2,x2=-
13
| ||
| 69 |
∵点M与点Q不重合,
∴x≠-2.
∴x=-
13
| ||
| 69 |
∴y=
| 2 |
| 3x |
26
| ||
| 3 |
∴点M的坐标为(-
13
| ||
| 69 |
26
| ||
| 3 |
点评:本题考查了用待定系数法求一次函数及反比例函数的解析式,考查了通过解方程组求一次函数与反比例函数图象的交点,考查了运用锐角三角函数和勾股定理解三角形,综合性比较强.通过解三角形求出AB长,从而求出直线QM与y轴交点B的坐标是解决第二小题的关键.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
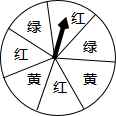 如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为
如图,一个转盘被分成7个相同的扇形,颜色分为红、黄、绿三种,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向红色的概率为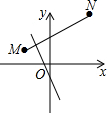 如图,在平面直角坐标系中,线段MN的端点坐标为M(-2,1),N(2,3),直线y=kx-1与线段MN有交点,则k的值不可能是( )
如图,在平面直角坐标系中,线段MN的端点坐标为M(-2,1),N(2,3),直线y=kx-1与线段MN有交点,则k的值不可能是( )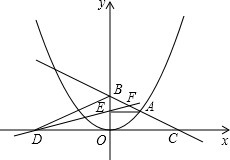 如图,在平面直角坐标系中,A是抛物线y=
如图,在平面直角坐标系中,A是抛物线y=
 如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)
如图,在教学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5米的测角仪AB,测得旗杆顶端D的仰角为32°,AC=22米,求旗杆CD的高度.(结果精确到0.1米.参考数据:sin32°≈0.53,cos32°≈0.85,tan32°≈0.62)