题目内容
9. 在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为6,△BCF的面积为9,△CEF的面积为6,则四边形ADFE的面积为24.
在△ABC中,点D,E分别在AB,AC上,且CD与BE相交于点F,已知△BDF的面积为6,△BCF的面积为9,△CEF的面积为6,则四边形ADFE的面积为24.
分析 可设S△ADF=m,根据题中条件可得出三角形的面积与边长之间的关系,进而用m表示出△AEF,求出m的值,进而可得四边形的面积.
解答 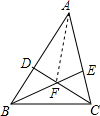 解:如图,连AF,设S△ADF=m,
解:如图,连AF,设S△ADF=m,
∵S△BDF:S△BCF=6:9=2:3=DF:CF,
则有$\frac{3}{2}$m=S△AEF+S△EFC,
S△AEF=$\frac{3}{2}$m-6,
而S△BFC:S△EFC=9:6=3:2=BF:EF,
又∵S△ABF:S△AEF=BF:EF=3:2,
而S△ABF=m+S△BDF=m+6,
∴S△ABF:S△AEF=BF:EF=3:2=(m+6):($\frac{3}{2}$m-6),
解得m=12.
S△AEF=12,
SADEF=S△AEF+S△ADF=12+12=24.
故答案为:24.
点评 本题主要考查了三角形的面积计算问题,能够利用三角形的性质进行一些简单的计算.

练习册系列答案
相关题目
1.下列说法正确的是( )
| A. | 4的平方根是-2 | B. | 8的立方根是±2 | ||
| C. | 任何实数都有平方根 | D. | 任何实数都有立方根 |
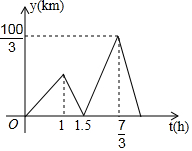 不览夜景,未到重庆.山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一.在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为t(h),快艇和轮船之间的距离为y(km),y与t的函数关系式如图所示.问快艇与轮船第二次相遇时到朝天门码头的距离为55千米.
不览夜景,未到重庆.山城夜景,早在清乾隆时期就已有名气,被时任巴县知县王尔鉴,列为巴渝十二景之一.在朝天门码头坐船游两江(即长江、嘉陵江),是游重庆赏夜景的一个经典项目.一艘轮船从朝天门码头出发匀速行驶,1小时后一艘快艇也从朝天门码头出发沿同一线路匀速行驶,当快艇先到达目的地后立刻按原速返回并在途中与轮船第二次相遇.设轮船行驶的时间为t(h),快艇和轮船之间的距离为y(km),y与t的函数关系式如图所示.问快艇与轮船第二次相遇时到朝天门码头的距离为55千米.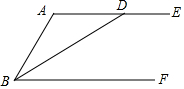 已知BD平分∠ABF,且交AE于点D.
已知BD平分∠ABF,且交AE于点D.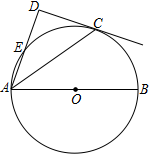 如图,点C在以AB为直径的⊙O上,AC平分∠DAB,AD与过点C的直线垂直,垂足为点D,AD交⊙O于点E.
如图,点C在以AB为直径的⊙O上,AC平分∠DAB,AD与过点C的直线垂直,垂足为点D,AD交⊙O于点E.