题目内容
16.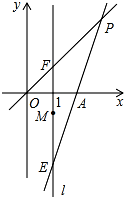 如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,F,M都在直线l上,且点E和点F关于点M对称.若点M坐标为(1,-1),直线EA与直线OF交于点P.
如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,F,M都在直线l上,且点E和点F关于点M对称.若点M坐标为(1,-1),直线EA与直线OF交于点P.(1)当点F的坐标为(1,1)时,如图,求点P的坐标;
(2)当点F为直线l上的动点时,记点P(x,y),求y关于x的函数解析式.
分析 (1)利用对称的性质得到E(1,-3),再利用待定系数法求出直线EA的解析式为y=3x-6.直线OF的解析式为y=x,利用两直线相交的问题,通过解方程组$\left\{\begin{array}{l}{y=x}\\{y=3x-6}\end{array}\right.$可得到点P的坐标;
(2)由已知可设点F的坐标是(1,t),与(1)一样,利用对称的性质得到E(1,-2-2t),再利用待定系数法求出直线EA的解析式为y=(2+t)x-4-2t,直线OF的解析式为y=tx,利用两直线相交的问题得到tx=(2+t)x-2(2+t),即t=x-2,于是得到y=tx=(x-2)x=x2-2x.
解答 解:(1)∵点E和点F关于点M(1,-1)对称,
而F(1,1),
∴E(1,-3),
设直线EA的解析式为:y=kx+b(k≠0)、
把E(1,-3),A(2,0)代入得$\left\{\begin{array}{l}{k+b=-3}\\{2k+b=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=3}\\{b=-6}\end{array}\right.$,
∴直线EA的解析式为:y=3x-6.
∵点O(0,0),F(1,1),
∴直线OF的解析式为y=x,
解方程组$\left\{\begin{array}{l}{y=x}\\{y=3x-6}\end{array}\right.$得$\left\{\begin{array}{l}{x=3}\\{y=3}\end{array}\right.$,
∴点P的坐标是(3,3);
(2)由已知可设点F的坐标是(1,t).
∴直线OF的解析式为y=tx,
由点E和点F关于点M(1,-1)对称,得点E(1,-2-t).
设直线EA的解析式为y=cx+d(c、d是常数,且c≠0),
把E(1,-2-t),A(2,0)代入得$\left\{\begin{array}{l}{c+d=-2-t}\\{2c+d=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{c=2+t}\\{d=-4-2t}\end{array}\right.$,
∴直线EA的解析式为:y=(2+t)x-4-2t,
∵点P为直线OF与直线EA的交点,
∴tx=(2+t)x-2(2+t),即t=x-2.
∴y=tx=(x-2)x=x2-2x.
点评 本题考查了两直线相交或平行问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.也考查了待定系数法求一次函数解析式.

| A. | 必然事件 | B. | 随机事件 | C. | 确定事件 | D. | 不可能事件 |
| A. | 58° | B. | 148° | C. | 158° | D. | 32° |
 如图,在⊙O中,∠BOC=100°,则∠A的度数是50°.
如图,在⊙O中,∠BOC=100°,则∠A的度数是50°. 如图,在△ABC中,AB=AC,D点在BA的延长线上,点E在AC上,且AD=AE,DE的延长线交BC于点F,求证:DF⊥BC.
如图,在△ABC中,AB=AC,D点在BA的延长线上,点E在AC上,且AD=AE,DE的延长线交BC于点F,求证:DF⊥BC. 把一张长方形纸片ABCD按如图所示的那样折叠后,若得到∠AEB′=56°,则∠BEF=62°.
把一张长方形纸片ABCD按如图所示的那样折叠后,若得到∠AEB′=56°,则∠BEF=62°.