题目内容
7. 如图,在△ABC中,AB=AC,D点在BA的延长线上,点E在AC上,且AD=AE,DE的延长线交BC于点F,求证:DF⊥BC.
如图,在△ABC中,AB=AC,D点在BA的延长线上,点E在AC上,且AD=AE,DE的延长线交BC于点F,求证:DF⊥BC.
分析 过A作AM⊥BC于M,根据等腰三角形三线合一的性质得出∠BAC=2∠BAM,由三角形外角的性质及等边对等角的性质得出∠BAC=2∠D,则∠BAM=∠D,根据平行线的判定得出DF∥AM,进而得到DF⊥BC.
解答  证明:如图,过A作AM⊥BC于M,
证明:如图,过A作AM⊥BC于M,
∵AB=AC,
∴∠BAC=2∠BAM,
∵AD=AE,
∴∠D=∠AED,
∴∠BAC=∠D+∠AED=2∠D,
∴∠BAC=2∠BAM=2∠D,
∴∠BAM=∠D,
∴DF∥AM,
∵AM⊥BC,
∴DF⊥BC.
点评 本题考查了等腰三角形的性质,三角形外角的性质,平行线的判定等知识,难度适中.准确作出辅助线是解题的关键.

练习册系列答案
相关题目
15.为开展阳光体育活动,某校组织了八年级五个班的足球赛,为更清楚地表示出首轮比赛中各班的总进球数,我们最好选择( )
| A. | 折线统计图 | B. | 条形统计图 | C. | 扇形统计图 | D. | 以上三种都可以 |
12. 如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
 如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )
如图,DE∥BC,且AD=4,DB=2,DE=3.5,则BC的长度为( )| A. | 5.5 | B. | 5.25 | C. | 6.5 | D. | 7 |
 如图,已知A(-2,4),B(4,2),C(2,-1)
如图,已知A(-2,4),B(4,2),C(2,-1) 如图,AB与CD相交于点O,且∠OAD=∠OCB,延长AD、CB交于点P,那么图中的相似三角形的对数为4.
如图,AB与CD相交于点O,且∠OAD=∠OCB,延长AD、CB交于点P,那么图中的相似三角形的对数为4.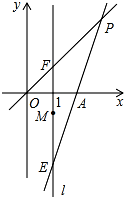 如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,F,M都在直线l上,且点E和点F关于点M对称.若点M坐标为(1,-1),直线EA与直线OF交于点P.
如图,在平面直角坐标系中,O为原点,直线l:x=1,点A(2,0),点E,F,M都在直线l上,且点E和点F关于点M对称.若点M坐标为(1,-1),直线EA与直线OF交于点P.