题目内容
19．两个相似多边形的面积之比为5，周长之比为m，则$\frac{5}{m}$为（ ）| A． | 1 | B． | $\frac{\sqrt{5}}{5}$ | C． | $\sqrt{5}$ | D． | 5 |
分析 根据相似三角形的性质：相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方，可以先求出m的值，再求$\frac{5}{m}$的值即可．
解答 解：∵两个相似多边形面积之比为5，周长之比为m，
∴由相似三角形的性质可得：5=m2，
解得m=±$\sqrt{5}$，
∵m=-$\sqrt{5}$不符合题意，
∴m=$\sqrt{5}$，
∴$\frac{5}{m}$=$\frac{5}{\sqrt{5}}$=$\sqrt{5}$．
故选C．
点评 本题考查了相似三角形的性质，牢记“相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方”是解题的关键．
练习册系列答案
相关题目
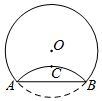如图，将半径为3cm的圆形纸片折叠后，劣弧中点C恰好与圆心O距离1cm，则折痕AB的长为2$\sqrt{5}$cm．
如图，已知长方形ABCD，E为BC边上的一点，现将△ABE沿AE翻折，翻折后点B恰好落在边DC上点F处．