题目内容
14.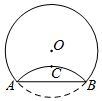 如图,将半径为3cm的圆形纸片折叠后,劣弧中点C恰好与圆心O距离1cm,则折痕AB的长为2$\sqrt{5}$cm.
如图,将半径为3cm的圆形纸片折叠后,劣弧中点C恰好与圆心O距离1cm,则折痕AB的长为2$\sqrt{5}$cm.
分析 连接OC并延长交⊙O于D,交AB于E,由点C是劣弧AB的中点,得到OC⊥AB,AE=BE,根据勾股定理即可得到结论.
解答  解:连接OC并延长交⊙O于D,交AB于E,
解:连接OC并延长交⊙O于D,交AB于E,
∵点C是劣弧AB的中点,
∴OC⊥AB,AE=BE,
∵OD=3,OC=1,
∴CE=DE=1,
∴OE=2,
∴AE=$\sqrt{O{A}^{2}-O{E}^{2}}$=$\sqrt{5}$,
∴AB=$2\sqrt{5}$cm;
故答案为:2$\sqrt{5}$.
点评 本题考查的是翻折变换,垂径定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
19.两个相似多边形的面积之比为5,周长之比为m,则$\frac{5}{m}$为( )
| A. | 1 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\sqrt{5}$ | D. | 5 |
6.下列汽车标志不是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
13.观察如图相应推理,其中正确的是( )
| A. |  ∵$\widehat{AD}$=$\widehat{BC}$ ∴AB=CD | B. | 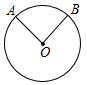 ∵$\widehat{AB}$的度数为40° ∴∠AOB=80° | ||
| C. | 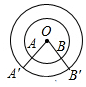 ∵∠AOB=∠A′OB′ ∴$\widehat{AB}$=$\widehat{A′B′}$ | D. | 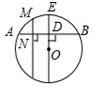 ∵MN垂直平分AD ∴$\widehat{MA}$=$\widehat{ME}$ |
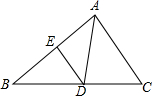 如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.
如图,△ABC中,D是BC上一点,∠DAC=∠B,E为AB上一点.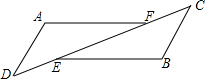 如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.
如图△ADF和△BCE中,∠A=∠B,点D、E、F、C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF. 小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象.
小明从家去体育场锻炼,同时,妈妈从体育场以50米/分的速度回家,小明到体育场后发现要下雨,立即返回,追上妈妈后,小明以250米/分的速度回家取伞,立即又以250米/分的速度折回接妈妈,并一同回家.如图是两人离家的距离y(米)与小明出发的时间x(分)之间的函数图象.