Question

2．如图，矩形ABCD中，AB=$\sqrt{6}$，AD=5，点P在AD上，当∠BPC=90°时，AP的长为2或3．

Answer 1

分析 连接BP、CP，设AP=x，表示出PD，再根据同角的余角相等求出∠ABP=∠DPC，然后求出△ABP和△DPC相似，根据相似三角形对应边成比例列式求解即可．

解答 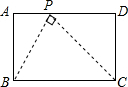解：如图，连接BP、CP，设AP=x，则PD=AD-AP=5-x，
在矩形ABCD中，∠A=∠D=90°，
所以，∠ABP+∠APB=90°，
∵∠BPC=90°，
∴∠APB+∠DPC=90°，
∴∠ABP=∠DPC，
∴△ABP∽△DPC，
∴$\frac{AB}{PD}$=$\frac{AP}{CD}$，
$\frac{\sqrt{6}}{5-x}$=$\frac{x}{\sqrt{6}}$，
整理得，x²-5x+6=0，
解得x₁=2，x₂=3，
所以，AP的长为2或3．
故答案为：2或3．

点评 本题考查了矩形的性质，相似三角形的判定与性质，确定出相似三角形是解题的关键．