题目内容
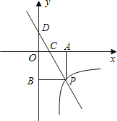
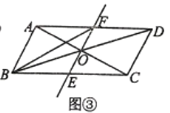
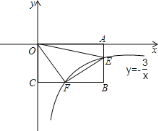
【题目】如图，反比例函数
图象经过矩形
边
的中点
，交边
于
点，连接
、
、
，则
的面积是（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
连接OB．首先根据反比例函数的比例系数k的几何意义，得出S△AOE=S△COF=1.5，然后由三角形任意一边的中线将三角形的面积二等分及矩形的对角线将矩形的面积二等分，得出F是BC的中点，则S△BEF=
S△OCF=0.75，最后由S△OEF=S矩形AOCB﹣S△AOE﹣S△COF﹣S△BEF，得出结果．
连接OB．
∵E、F是反比例函数y=﹣
（x＞0）图象上的点，EA⊥x轴于A，FC⊥y轴于C，∴S△AOE=S△COF=1.5．
∵矩形OABC边AB的中点是E，∴S△BOE=S△AOE=1.5，S△BOC=S△AOB=3，∴S△BOF=S△BOC﹣S△COF=3﹣1.5=1.5，∴F是BC的中点，∴S△OEF=S矩形AOCB﹣S△AOE﹣S△COF﹣S△BEF=6﹣1.5﹣1.5﹣0.5×1.5=
．
故选B．
练习册系列答案
芒果教辅达标测试卷系列答案
相关题目
