题目内容
13. 如图,已知:在矩形ABCD中,DF平分∠ADC,交AC于E,交BC于F,∠BDF=15°,求:∠ODC和∠BOF的度数.
如图,已知:在矩形ABCD中,DF平分∠ADC,交AC于E,交BC于F,∠BDF=15°,求:∠ODC和∠BOF的度数.
分析 根据DF平分∠ADC与∠BDF=15°可以计算出∠ODC=60°,再根据矩形的对角线相等且互相平分可得OD=OC,从而得到△OCD是等边三角形,再证明△COF是等腰三角形,求出∠CFO=75°,即可得出∠BOF的度数.
解答 解:∵DF平分∠ADC,
∴∠CDF=45°,
∴△CDF是等腰直角三角形,
∴CD=CF.
∵∠BDF=15°,
∴∠ODC=∠CDF+∠BDF=45°+15°=60°,
在矩形ABCD中,OD=OC,
∴△OCD是等边三角形,
∴OC=CD,∠OCD=∠COD=60°,
∴OC=CF,∠BOC=120°,∠OCF=90°-∠OCD=90°-60°=30°,
在△COF中,∠CFO=$\frac{1}{2}$(180°-30°)=75°,
∴∠BOF=∠BOC-∠CFO=120°-75°=45°.
点评 本题考查了矩形的性质,等边三角形的判定与性质,等腰三角形的性质,角平分线的定义,邻补角的性质,三角形内角和定理,熟记各性质并判断出△OCD是等边三角形是解决本题的关键.

练习册系列答案
相关题目
4.将正整数依次按如表规律排成四列,请根据表中的排列规律回答下列问题:
(1)第6行第2列的数是多少?
(2)用含n的代数式表示第n行第3列的数;
(3)数2016位于第几行第几列?
| 第1列 | 第2列 | 第3列 | 第4列 | |
| 第1行 | 1 | 2 | 3 | |
| 第2行 | 6 | 5 | 4 | |
| 第3行 | 7 | 8 | 9 | |
| 第4行 | 12 | 11 | 10 | |
| … |
(2)用含n的代数式表示第n行第3列的数;
(3)数2016位于第几行第几列?
3. 如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
 如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )
如图,△ABC中,∠B=90°,AB=1,BC=2,则sinA=( )| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{1}{2}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{{\sqrt{5}}}{5}$ |
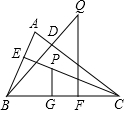 已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.
已知:如图,在锐角△ABC中,BD,CE分别是△ABC的AC,AB边上的高,在CE上截取CP=AB,过点P作PG⊥BC于G点,在BD的延长线上截取BQ=AC,过点Q作QF⊥BC于F点,求证:PG+QF=BC.