题目内容
 阅读理解题:
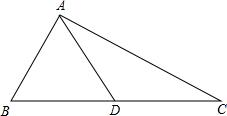
阅读理解题:如图,在△ABC中,AD是BC边上的中线,且AD=
| 1 |
| 2 |
求证:∠BAC=90°.
证明:∵AD=:∵AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=BD=DC,
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,
即∠BAC=90°.
此题实际上是判断一个三角形是不是直角三角形的一种方法,请你用文字语言叙述出来.
考点:直角三角形斜边上的中线
专题:阅读型
分析:根据题目的已知条件和结论写出判断方法即可.
解答:解:用文字叙述为:如果三角形一条边上的中线等于这条边的一半,那么这个三角是直角三角形.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质的逆命题的证明,从已知和求证寻找条件和结论是写出命题的关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
下列关于倒数说法错误的是( )
| A、正数的倒数是正数 |
| B、负数的倒数是负数 |
| C、零的倒数是零 |
| D、倒数等于本身的数只有1和-1 |
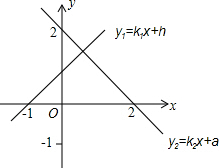 已知一次函数y1=k1x+b与y2=k2x+a的图象如图所示:
已知一次函数y1=k1x+b与y2=k2x+a的图象如图所示: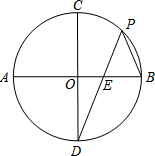 如图,⊙O中,直径AB⊥CD于O点,P为
如图,⊙O中,直径AB⊥CD于O点,P为
 如图所示,在圆O中,
如图所示,在圆O中,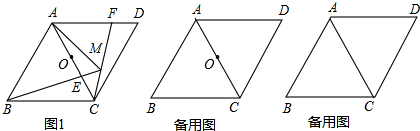
 如图,AB=DE=GH=MN=2,其余各短边长为1,且图中的角都是直角,请建立适当的直角坐标系,并写出各个顶点的坐标.
如图,AB=DE=GH=MN=2,其余各短边长为1,且图中的角都是直角,请建立适当的直角坐标系,并写出各个顶点的坐标.